(本題滿分14分)已知函數(shù)
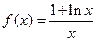

(1)若函數(shù)在區(qū)間
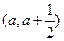
上存在極值,其中
a >0,求實數(shù)
a的取值范圍;
(2)如果當
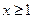
時,不等式
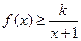
恒成立,求實數(shù)
k的取值范圍;
(3)求證:
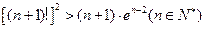
。
(1)

(2)
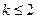
(3)略

(2)不等式

即為
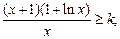
記
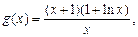
所以
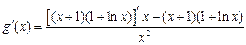
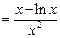
………… 6分
令
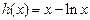
,則
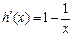
,
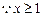
,
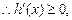

在
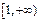
上單調(diào)遞增,
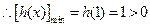
,從而
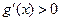
, 故
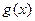
在
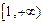
上也單調(diào)遞增,………… 8分
所以
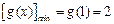
,所以
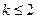
.


………… 9分
(3)由(2)知:

恒成立,即
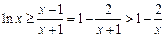
,
令
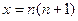
,則
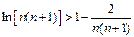
, ………… 11分
所以
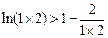
,
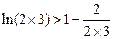
,
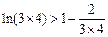
,
… …

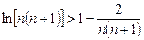
,
疊加得:
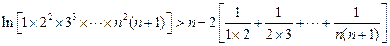

=n-2(1-
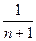
)>n-2+
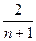
>n-2 . ………… 13分
則
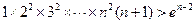
,所以[(n+1)!]
2>(n+1).e
n-2(n∈N
*)………… 14分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知函數(shù)
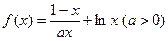
.
(1)若函數(shù)f(x)在
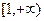
上為增函數(shù),求實數(shù)a的取值范圍;
(2)當a=1時,求f(x)在
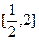
上的最大值和最小值;(注
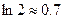
)
(3)當a=1時,求證:對大于1的任意正整數(shù)n,均有
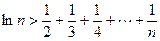
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
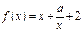
(
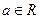
)
(1)若
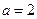
,求
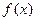
在
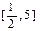
上的最小值和最大值;
(2)如果
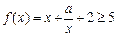
對
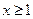
恒成立,求實數(shù)
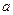
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)
f0(
x) =
sinx,
f1(
x)=
f0′(
x),
f2(
x)=
f1′(
x),…,
fn+1(
x) =
fn′(
x),
n∈N,則
f2005(
x)=
| A.sinx | B.-sinx | C.cosx | D.-cosx |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)f(x)=sin x+ln x,則f′(1)的值為 ( )
A 1-cos1 B 1+cos1 C cos1-1 D -1-cos1
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若函數(shù)
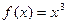
,導函數(shù)值
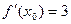
,則正數(shù)
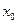
的值
為
▲ .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)

,且

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
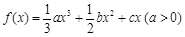
,記
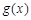
為它的導函數(shù),若
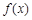
在R上存在反函數(shù),且
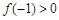
,則
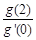
的最小值為( )
| A.4 | B.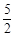 | C.2 | D.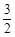 |
查看答案和解析>>

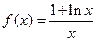

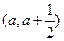 上存在極值,其中a >0,求實數(shù)a的取值范圍;
上存在極值,其中a >0,求實數(shù)a的取值范圍;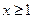 時,不等式
時,不等式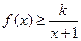 恒成立,求實數(shù)k的取值范圍;
恒成立,求實數(shù)k的取值范圍;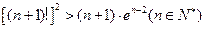 。
。 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案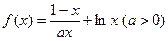 .
.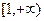 上為增函數(shù),求實數(shù)a的取值范圍;
上為增函數(shù),求實數(shù)a的取值范圍;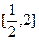 上的最大值和最小值;(注
上的最大值和最小值;(注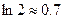 )
)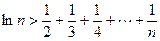 .
.