
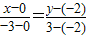 ,即5x+3y+6=0;(4分)
,即5x+3y+6=0;(4分)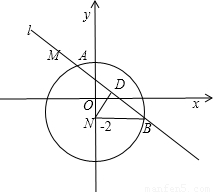
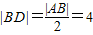 ,(6分)
,(6分)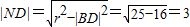 ,(10分)
,(10分) ,
,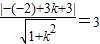 ,解得:
,解得: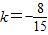 ,
,

 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2010年河北省邯鄲市高二上學期期末考試數學理卷 題型:解答題
(示范高中)如圖,已知橢圓 (a>b>0)的離心率
(a>b>0)的離心率 ,過點
,過點 和
和 的直線與原點的距離為
的直線與原點的距離為 .
.
(1)求橢圓的方程;
(2)已知定點 ,若直線
,若直線 與橢圓交于
與橢圓交于 、
、 兩點.問:是否存在
兩點.問:是否存在 的值,使以
的值,使以 為直徑的圓過
為直徑的圓過 點?請說明理由.
點?請說明理由.

查看答案和解析>>
科目:高中數學 來源:2010年河北省邯鄲市高二上學期期末考試數學理卷 題型:解答題
(示范高中做)(本題滿分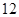 分)已知雙曲線
分)已知雙曲線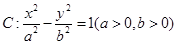 的離心率為
的離心率為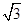 ,且雙曲線上點到右焦點的距離與到直線
,且雙曲線上點到右焦點的距離與到直線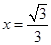 的距離之比為
的距離之比為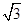
(1) 求雙曲線 的方程;
的方程;
(2)已知直線 與雙曲線
與雙曲線 交于不同的兩點
交于不同的兩點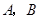 ,且線段
,且線段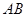 的中點在圓
的中點在圓 上,求
上,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省揚大附中高二(上)期中數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com