
(07年湖北卷文)(12分)
如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,且
的中點,且![]() ,
,![]() .
.
(I)求證:平面![]() 平面
平面![]() ;
;
(II)試確定角![]() 的值,使得直線
的值,使得直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.

本小題主要考查線面關(guān)系、直線與平面所成角的有關(guān)知識,考查空間想象能力和推理運算能力以及應用向量知識解決數(shù)學問題的能力.
解析:解法1:(Ⅰ)![]() ,
,![]() 是等腰三角形,又
是等腰三角形,又![]() 是
是![]() 的中點,
的中點,
![]() ,又
,又![]() 底面
底面![]() .
.![]() .于是
.于是![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ) 過點![]() 在平面
在平面![]() 內(nèi)作
內(nèi)作![]() 于
于![]() ,則由(Ⅰ)知
,則由(Ⅰ)知![]() 平面
平面![]() .
.
連接![]() ,于是
,于是![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成的角.
所成的角.
依題意![]() ,所以
,所以
在![]() 中,
中,![]() ;
;
在![]() 中,
中,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
故當![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.
解法2:(Ⅰ)以![]() 所在的直線分別為
所在的直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸,建立如圖所示的空間直角坐標系,
軸,建立如圖所示的空間直角坐標系,
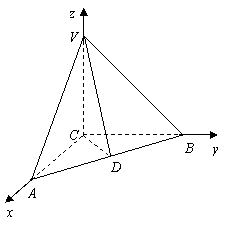
則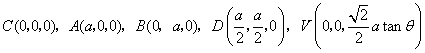 ,
,
于是,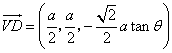 ,
,![]() ,
,![]() .
.
從而![]() ,即
,即![]() .
.
同理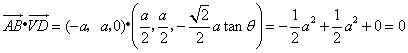 ,
,
即![]() .又
.又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則由![]() .
.
得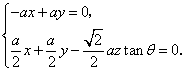
可取![]() ,又
,又![]() ,
,
于是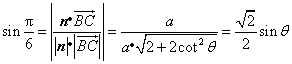 ,
,
即![]()
![]() ,
,![]() .
.
故交![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.
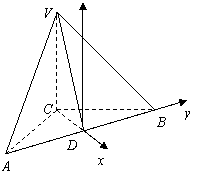
解法3:(Ⅰ)以點![]() 為原點,以
為原點,以![]() 所在的直線分別為
所在的直線分別為![]() 軸、
軸、![]() 軸,建立如圖所示的空間直角坐標系,
軸,建立如圖所示的空間直角坐標系,
則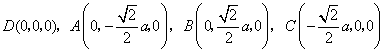 ,
,
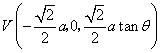 ,于是
,于是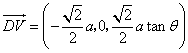 ,
,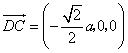 ,
,![]() .
.
從而![]()
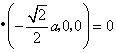 ,即
,即![]() .
.
同理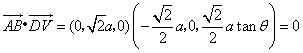 ,即
,即![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則由![]() ,得
,得
可取![]() ,又
,又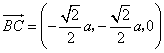 ,
,
于是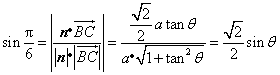 ,
,
即![]() .
.
故交![]() 時,
時,
即直線![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案科目:高中數(shù)學 來源: 題型:
(07年湖北卷文)為了了解學校學生的身體發(fā)育情況,抽查了該校100名高中男生的體重情況,根據(jù)所得數(shù)據(jù)畫出樣本的頻率分布直方圖如圖所示,根據(jù)此圖,估計該校2000名高中男生中體重大于70.5公斤的人數(shù)為
A.300 B.350
C.420 D.450

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com