
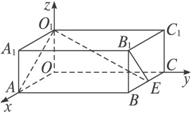
(1)求O1E的長;
(2)求直線AO1與B1E所成的角.
解法一:(1)![]() =
= ![]() +
+![]() =
=![]() .
.
∴|![]() |2=(
|2=(![]() +
+![]() +
+![]()
![]() )2=|
)2=|![]() |2+|
|2+|![]() |2+|
|2+|![]()
![]() |2=4+9+1=14.
|2=4+9+1=14.
∴|![]() |=14.
|=14.
(2) ![]() =-
=-![]() +
+![]() ,
,![]() =
=![]() +
+![]() =
=![]() -
-![]()
![]() .
.
![]() ·
·![]() =(-
=(-![]() +
+![]() )·(
)·(![]() -
-![]()
![]() )=
)= ![]() |
|![]() |2-|
|2-|![]() |2=-2.
|2=-2.
|![]() |=
|=![]() .
.
|![]() |=
|=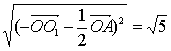 .
.
∴cos〈![]() ,
,![]() 〉=
〉=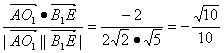 .
.
∴〈![]() ,
,![]() 〉=arccos(-
〉=arccos(-![]() )=π-arccos
)=π-arccos![]() .
.
故![]() 與
與![]() 所成的角為arccos
所成的角為arccos![]() .
.
解法二:以O(shè)A作為x軸正軸,OC作為y軸正軸,OO1作為z軸正軸,建立空間直角坐標(biāo)系.

(1)O1(0,0,2),E(1,3,0),
∴|![]() |=
|=![]() .
.
(2)A(2,0,0),B1(2,3,2),則![]() =(-2,0,2),
=(-2,0,2),![]() =(-1,0,-2).
=(-1,0,-2).
∴![]() ·
·![]() =(-2)×(-1)+2×(-2)=-2,
=(-2)×(-1)+2×(-2)=-2,
|![]() |=
|=![]() ,|
,| ![]() |=
|=![]() .
.
∴cos〈![]() ,
, ![]() 〉=
〉=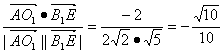 .
.
故AO1與B1E1所成的角為arccos![]() .
.
解法三:(1)連結(jié)OE,
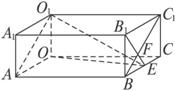
在Rt△OEC中,
OE=![]() .
.
又由O1O⊥平面OABC知O1O⊥OE,
在Rt△O1OE中,O1E=![]() .
.
(2)連結(jié)BC1,交B1E于F,
則BC1∥AO1.
設(shè)∠BFE=β,∠BEF=α,
則β即為直線AO1與B1E所成的角.
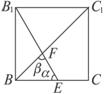
依題意,側(cè)面B1BCC1為正方形,
在Rt△B1BE中,tanα=2,B1E=![]() ,sinα=
,sinα=![]() ,cosα=
,cosα=![]() .
.
∴α=arcsin![]() 或arccos
或arccos![]() 或arctan2.
或arctan2.
∴β=π-![]() -α=
-α=![]() -arcsin
-arcsin![]() (或β=
(或β=![]() -arccos
-arccos![]() 或β=
或β=![]() -arctan2).
-arctan2).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
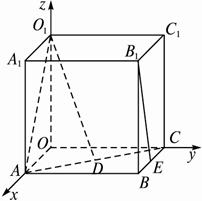
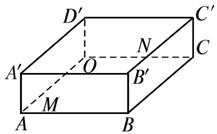
(1)求直線AO1與B1E所成角的大小;
(2)作O1D⊥AC于D.求點(diǎn)O1到點(diǎn)D的距離.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com