
球面上有三個點A、B、C. A和B,A和C間的球面距離等于大圓周長的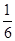 . B和C間的球面距離等于大圓周長的
. B和C間的球面距離等于大圓周長的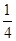 .如果球的半徑是R,那么球心到截面ABC的距離等于( )
.如果球的半徑是R,那么球心到截面ABC的距離等于( )
A.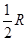 B.
B. 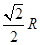 C.
C. 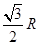 D.
D. 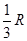
B
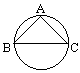
解析試題分析:如圖所示,圓O是球的大圓,且大圓所在平面與面ABC垂直,其中弦EF是過A、B、C的小圓的直徑,弦心距OD就是球心O到截面ABC的距離,OE是球的半徑,因此,欲求OD,需先求出截面圓ABC的半徑.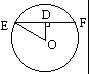
下一個圖是過A、B、C的小圓.AB、AC、CB是每兩點之間的直線段.它們的長度要分別在△AOB、△AOC、△COB中求得(O是球心).由于A、B間球面距離是大圓周長的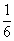 ,所以∠AOB=
,所以∠AOB=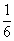 ×2π=
×2π=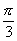 ,同理∠AOC=
,同理∠AOC=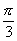 ,∠BOC=
,∠BOC=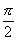 .
. 
∴|AB|=R, |AC|=R, |BC|=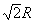 .在△ABC中,由于AB2+AC2=BC2.∴∠BAC=90°,BC是小圓ABC的直徑. ∴|ED|=
.在△ABC中,由于AB2+AC2=BC2.∴∠BAC=90°,BC是小圓ABC的直徑. ∴|ED|=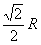 ,從而|OD|=
,從而|OD|=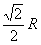 .故應選B.
.故應選B.
考點:點到平面的距離;球的有關性質。
點評:本題考查球面距離的概念及學生的空間想像能力以及對球的性質認識及利用,有關幾何體的外接球,是常考知識點,也是難點,我們在平常做題時應注意總結。


科目:高中數學 來源: 題型:單選題
圓C1 :(x+1)2+(y+4)2=16與圓C2 : (x-2)2+(y+2)2=9的位置關系是( ).
| A.相交 | B.外切 | C.內切 | D.相離 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
如圖,在平面直角坐標系中, 是一個與x軸的正半軸、y軸的正半軸分別相切于點C、D的定圓所圍成區域(含邊界),A、B、C、D是該圓的四等分點,若點P(x,y)、
是一個與x軸的正半軸、y軸的正半軸分別相切于點C、D的定圓所圍成區域(含邊界),A、B、C、D是該圓的四等分點,若點P(x,y)、 ,則稱P優于
,則稱P優于 ,如果
,如果 中的點Q滿足:不存在
中的點Q滿足:不存在 中的其它點優于Q,那么所有這樣的點Q組成的集合是劣弧( )
中的其它點優于Q,那么所有這樣的點Q組成的集合是劣弧( )
A. A B.B C. C D.D
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com