
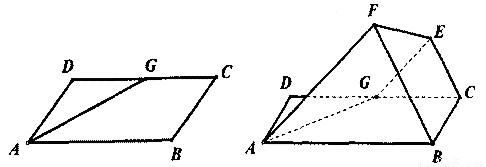
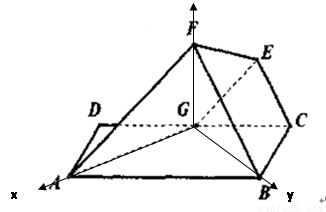
如圖,己知平行四邊形ABCD中,∠ BAD = 600,AB=6, AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG。
(I)求證:直線CE//平面ABF;
(II)如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值.
(Ⅲ)若直線AF與平面 ABCD所成角為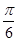 ,求證:FG⊥平面ABCD
,求證:FG⊥平面ABCD
(1)見解析;(2)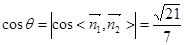 ;(3)見解析.
;(3)見解析.
【解析】第一問中利用線面平行的判定定理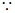 ABCD是平行四邊形,
ABCD是平行四邊形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF
CE//平面ABF
第二問中,因為AG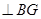 ,如圖建立空間直角坐標系
,如圖建立空間直角坐標系
(1)證明: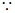 ABCD是平行四邊形,
ABCD是平行四邊形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF
 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF …………4分
CE//平面ABF …………4分
(2)AG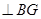 ,如圖建立空間直角坐標系
,如圖建立空間直角坐標系
設平面BFEC的法向量為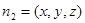 則
則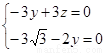
 平面AEF的法向量
平面AEF的法向量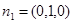
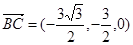

,利用數量積的公式得到二面角的表示。
第三問中,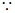
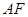 與平面ABCD所成的角為30゜,AF=6
與平面ABCD所成的角為30゜,AF=6  設F(x,y,3)
設F(x,y,3)
又FG=GB=3 
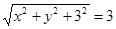

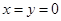
 F(0,0,3)
F(0,0,3)
 GF=(0,0,3)
GF=(0,0,3) GF
GF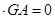
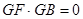

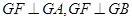

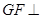 平面ABCD
平面ABCD
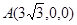
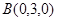
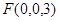
 平面AEF的法向量
平面AEF的法向量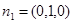
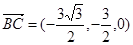

設平面BFEC的法向量為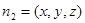 則
則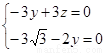

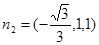

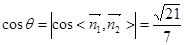 即為所求。……………10分
即為所求。……………10分
(3)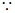
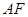 與平面ABCD所成的角為30゜,AF=6
與平面ABCD所成的角為30゜,AF=6  設F(x,y,3)
設F(x,y,3)
又FG=GB=3 
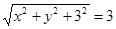

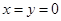
 F(0,0,3)
F(0,0,3)
 GF=(0,0,3)
GF=(0,0,3) GF
GF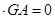
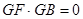

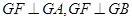

 平面ABCD…………15分
平面ABCD…………15分


科目:高中數學 來源: 題型:
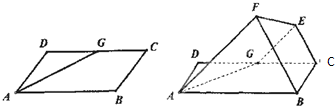 如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.
如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.查看答案和解析>>
科目:高中數學 來源: 題型:
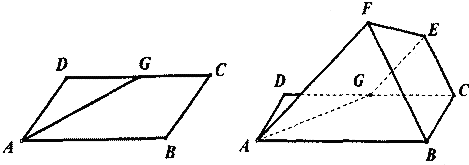 如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.
如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.
如圖,己知平行四邊形ABCD中,∠BAD=60°,AB=6,AD=3,G為CD中點,現將梯形ABCG沿著AG折起到AFEG.| π | 6 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省寧波市高三(下)4月月考數學試卷(文科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com