
(1)求實數b的取值范圍;
(2)若函數F(x)=logbf(x)在區間(-1-c,1-c)上具有單調性,求實數c的取值范圍.
(文)已知二次函數f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集為{x|-1≤x≤1},求實數b、c的值;
(2)若f(x)滿足f(1)=0,且關于x的方程f(x)+x+b=0的兩個實數根分別在區間(-3,-2)、(0,1)內,求實數b的取值范圍.
答案:(理)解:(1)由題,知f(1)=1+2b+c=0,∴c=-1-2b.
記g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,
則 即b∈(
即b∈(![]() ).
).
(2)令u=f(x).∵0<![]() <b<
<b<![]() <1,∴logbu在(0,+∞)上是減函數.而-1-c=2b>-b,函數f(x)=x2+2bx+c的對稱軸為x=-b,∴f(x)在區間(-1-c,1-c)上單調遞增.從而函數F(x)=logbf(x)在(-1-c,1-c)上為減函數.
<1,∴logbu在(0,+∞)上是減函數.而-1-c=2b>-b,函數f(x)=x2+2bx+c的對稱軸為x=-b,∴f(x)在區間(-1-c,1-c)上單調遞增.從而函數F(x)=logbf(x)在(-1-c,1-c)上為減函數.
且f(x)在區間(-1-c,1-c)上恒有f(x)>0,只需要f(-1-c)≥0,
∴ .
.
(文)解:(1)由題,知x1=-1,x2=1是方程x2+2bx+c=0的兩個根.
由韋達定理,得
即![]() ∴b=0,c=-1.
∴b=0,c=-1.
(2)由題,知f(1)=1+2b+c=0,∴c=-1-2b.2分記g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,則
 即b∈(
即b∈(![]() ,
,![]() ).
).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| 1 |
| 8 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年宜昌一中12月月考理)(14分)
已知二次函數![]() 。
。
(1)若對任意x1,x2∈R,且![]() ,都有
,都有![]() ,求證:關于x的方程
,求證:關于x的方程![]() 有兩個不相等的實數根且必有一個根屬于(
有兩個不相等的實數根且必有一個根屬于(![]() );
);
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
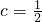 時,求出不等式f(x)<0的解;
時,求出不等式f(x)<0的解;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com