
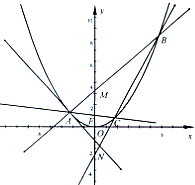
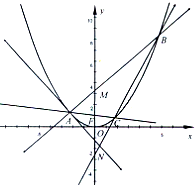
 如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.
如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.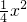 ,∴
,∴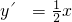 ,∴直線l的斜率k1=
,∴直線l的斜率k1=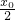
 ,∴直線AB的方程為y-y0=-
,∴直線AB的方程為y-y0=- (x-x0)
(x-x0) x2+
x2+ x-2-y0=0
x-2-y0=0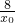 ,∴x1=-x0-
,∴x1=-x0-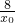
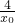
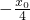 -
-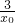 ,∴直線BC的方程為y-y2=(
,∴直線BC的方程為y-y2=(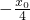 -
-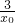 )(x-x2)
)(x-x2)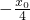 -
-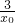 )(-x2)+y2,代入x2=-
)(-x2)+y2,代入x2=-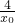 ,y2=
,y2=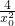 ,化簡得y=-1-
,化簡得y=-1-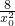
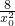 ),∴|MN|=y0+2+1+
),∴|MN|=y0+2+1+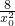 =
=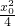 +
+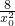 3≥3+2
3≥3+2 當且僅當x04=32時等號成立,
當且僅當x04=32時等號成立, .
.

科目:高中數學 來源: 題型:
 如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.
如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.查看答案和解析>>
科目:高中數學 來源: 題型:
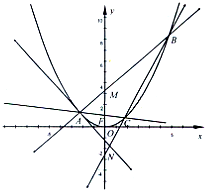 (2012•金華模擬)如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.
(2012•金華模擬)如圖,A是拋物線x2=4y上異于原點的任意一點,F為拋物線的焦點,l為拋物線在A點處的切線,點B、C在拋物線上,AB⊥l且交y軸于M,點A、F、C三點共線,直線BC交y軸于N.查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省嘉興一中高三(上)10月月考數學試卷(文科)(解析版) 題型:填空題
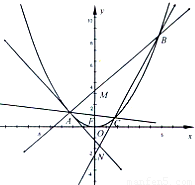
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省嘉興一中高三(上)10月月考數學試卷(文科)(解析版) 題型:填空題
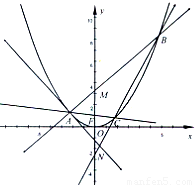
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com