設
AB是圓
x2+
y2=1的一條直徑,以
AB為直角邊、
B為直角頂點,逆時針方向作等腰直角三角形
ABC.當
AB變動時,求
C點的軌跡.

所求軌跡是以原點為圓心,

為半徑的圓.
解法一:(參數(shù)法)取∠
xOB=
θ為參數(shù),則
B(cos
θ,sin
θ),
于是,(
x-cos
θ)
2+(
y-sin
θ)
2=4.
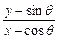
=-cot
θ,消去
θ得
x2+
y2=5.
故所求軌跡是以原點為圓心,

為半徑的圓.
解法二:(相關點法)設
C(
x,
y)、
B(
x0,
y0),
當
x0、
y0≠0時,
則(
x-
x0)
2+(
y-
y0)
2=4.
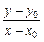
·
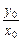
=-1.由
x02+
y02=1消去
x0、
y0得軌跡方程.顯然當
x0=0或
y0=0時,方程也適合.
解法三:(幾何法)連結
CO,因為|
OC|
2=|
OB|
2+|
AB|
2=5為定值,故其軌跡為圓.
評析:求軌跡的方法很多,注意合理選取,參數(shù)法求軌跡方程是常用方法之一,常用到的參數(shù)有斜率、點的坐標、長度、夾角等.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓

的圓心在直線

上,并且經過原點和

,
求圓

的標準方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
圓
C過點
P(1,2)和
Q(-2,3),且圓
C在兩坐標軸上截得的弦長相等,求圓
C的方程.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,圓O的兩弦AB和CD交于點E,
EF∥CB,EF交AD的延長線于點F,F(xiàn)G切圓O于點G.
(1)求證:△DFE∽△EFA;
(2)如果EF=1,求FG的長.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
求通過原點且與兩直線l1:x+2y-9=0,l2:2x-y+2=0相切的圓的 方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓在
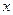
軸上兩個截距分別為
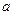
,
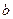
,在
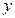
軸上的一個截距為
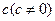
,試求此圓方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(
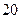
分)
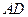
是直角三角形

斜邊

上的高,(
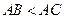
),
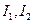
分別是
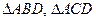
的內心,
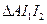
的外接圓
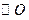
分別交

于
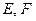
,直線
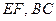
交于點
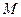
;證明:
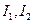
分別是
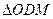
的內心與旁心.
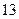
查看答案和解析>>


 為半徑的圓.
為半徑的圓.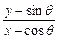 =-cotθ,消去θ得x2+y2=5.
=-cotθ,消去θ得x2+y2=5. 為半徑的圓.
為半徑的圓.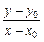 ·
·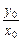 =-1.由x02+y02=1消去x0、y0得軌跡方程.顯然當x0=0或y0=0時,方程也適合.
=-1.由x02+y02=1消去x0、y0得軌跡方程.顯然當x0=0或y0=0時,方程也適合.

 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案