
解:注意到![]() +x=
+x=![]() ,即有lg(
,即有lg(![]() -x)=-lg(
-x)=-lg(![]() +x),從而f(-x)=lg(
+x),從而f(-x)=lg(![]() +x)=-lg(
+x)=-lg(![]() -x)=-f(x),可知其為奇函數.又因為奇函數在關于原點對稱的區間上的單調性相同,所以我們只需研究(0,+∞)上的單調性.
-x)=-f(x),可知其為奇函數.又因為奇函數在關于原點對稱的區間上的單調性相同,所以我們只需研究(0,+∞)上的單調性.
由題意![]() -x>0,解得x∈R,即定義域為R.
-x>0,解得x∈R,即定義域為R.
又f(-x)=lg[![]() -(-x)]=lg(
-(-x)]=lg(![]() +x)?
+x)?
=lg![]() =lg(
=lg(![]() -x) -1
-x) -1
=-lg(![]() -x)=-f(x).
-x)=-f(x).
∴y=lg(![]() -x)是奇函數.
-x)是奇函數.
任取x 1、x 2∈(0,+∞)且x 1<x 2,
則![]() <
<![]()
![]()
![]() +x 1<
+x 1<![]() +x 2
+x 2
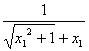 >
>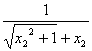 ,
,
即有![]() -x 1>
-x 1>![]() -x2>0,
-x2>0,
∴lg(![]() -x 1)>lg(
-x 1)>lg(![]() -x 2),
-x 2),
即f(x 1)>f(x 2)成立.?
∴f(x)在(0,+∞)上為減函數.?
又f(x)是定義在R上的奇函數,
故f(x)在(-∞,0)上也為減函數.


科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年貴州省高三年級第五次月考文科數學 題型:選擇題
已知函數y=lg(x+1)+3,(x>-1)則反函數為
(A) 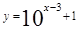 (x≥3)
(B)
(x≥3)
(B) 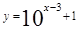 (x∈R)
(x∈R)
(C) 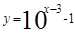 (x∈R) (D)
(x∈R) (D) 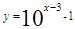 (x≥3)
(x≥3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com