
(1)判斷函數f(x)在區間(0,+∞)上的單調性,證明你的結論;
(2)若當x>0時,f(x)>![]() 恒成立,求正整數k的最大值.(參考數據:ln2≈0.7,ln3≈1.1)
恒成立,求正整數k的最大值.(參考數據:ln2≈0.7,ln3≈1.1)
(文) P1是橢圓![]() +y2=1(a>0且a≠1)上不與頂點重合的任一點,P1P2是垂直于x軸的弦,A1(-a,0),A2(a,0)是橢圓的兩個端點,直線A1P1與直線A2P2交點為P.
+y2=1(a>0且a≠1)上不與頂點重合的任一點,P1P2是垂直于x軸的弦,A1(-a,0),A2(a,0)是橢圓的兩個端點,直線A1P1與直線A2P2交點為P.
(1)求P點的軌跡曲線C的方程;
(2)設曲線C與直線l:x+y=1相交于兩個不同的點A、B,求曲線C的離心率e的取值范圍;
(3)設曲線C與直線l:x+y=1相交于兩個不同的點A、B,O為坐標原點,且![]() =-3,求a的值.
=-3,求a的值.
(理)解:(1)f′(x)=![]() [
[![]() -1-ln(x+1)]=
-1-ln(x+1)]=![]() [
[![]() +ln(x+1)],
+ln(x+1)],
∵x>0,∴x2>0,![]() >0,ln(x+1)>0.
>0,ln(x+1)>0.
∴f′(x)<0.
因此函數f(x)在區間(0,+∞)上是減函數.
(2)(方法1)當x>0時,f(x)>![]() 恒成立,令x=1有k<2(1+ln2).又k為正整數,
恒成立,令x=1有k<2(1+ln2).又k為正整數,
∴k的最大值不大于3.
下面證明當k=3時,f(x)>![]() (x>0)恒成立,
(x>0)恒成立,
即證當x>0時,(x+1)ln(x+1)+1-2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1-2x,則g′(x)=ln(x+1)-1,
當x>e-1時,g′(x)>0;當0<x<e-1時,g′(x)<0.
∴當x=e-1時,g(x)取得最小值g(e-1)=3-e>0.
∴當x>0時,(x+1)ln(x+1)+1-2x>0恒成立.
因此正整數k的最大值為3.
(方法2)當x>0,f(x)>![]() 恒成立.
恒成立.
h(x)=![]() >k對x>0恒成立.h(x)(x>0)的最小值大于k.
>k對x>0恒成立.h(x)(x>0)的最小值大于k.
h′(x)=![]() ,記φ(x)=x-1-ln(x+1)(x>0),
,記φ(x)=x-1-ln(x+1)(x>0),
則φ′(x)=![]() >0,
>0,
∴φ(x)在(0,+∞)上連續遞增.
又φ(2)=1-ln3<0,φ(3)=2-2ln2>0,
∴φ(x)=0存在唯一實根a,且滿足:a∈(2,3),即a-1-ln(a+1)=0.∴a=1+ln(a+1).
由x>a時,φ(x)>0,h′(x)>0;0<x<a時,φ(x)<0,h′(x)<0知:
h(x)(x>0)的最小值為h(a)=![]() =a+1.
=a+1.
又2<a<3,∴3<a+1<4,為使k<h(x)對于x>0恒成立,
因此正整數k的最大值為3.
(文)(1)解:設P1(m,n)(mn≠0),則P2(m,-n),
直線A1P1:y=![]() (x+a);①
(x+a);①
直線A2P2:y=![]() (x-a);②
(x-a);②
設P點坐標為(x,y),
由①②得m=![]() ,n=
,n=![]() ,
,
∵點P1(m,n)在橢圓![]() +y2=1上,
+y2=1上,
∴有m2+a2n2=a2,
即(![]() )2+a2(
)2+a2(![]() )2=a2,整理得
)2=a2,整理得![]() -y2=1(y≠0).
-y2=1(y≠0).
∴直線A1P1與直線A2P2交點P的軌跡方程是雙曲線![]() -y2=1(y≠0).
-y2=1(y≠0).
(2)由C與l相交于兩個不同的點,故知方程組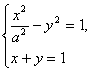 有兩個不同的實數解.消去y并整理得(1-a2)x2+2a2x-2a2=0.
有兩個不同的實數解.消去y并整理得(1-a2)x2+2a2x-2a2=0.
又∵a>0且a≠1,
∴4a4+8a2(1-a2)>0.
∴0<a2<2且a2≠1.
雙曲線的離心率e=![]() .
.
∴![]() <e<
<e<![]() 或e>
或e>![]() ,即e∈(
,即e∈(![]() )∪(
)∪(![]() ,+∞).
,+∞).
(3)設A(x1,y1)、B(x2,y2),
則-3=![]() =x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1=
=x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1=![]() +1,
+1,
即![]() =-4,由a>0,得a=
=-4,由a>0,得a=![]() .
.


科目:高中數學 來源: 題型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知函數f(x)=
已知函數f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| x-1 | x+a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com