
已知:0<a<b<c<d 且a+d=b+c,求證: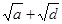 <
< 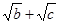
見解析
解析試題分析:
直接證明顯然不容易入手,所以采用分析法證明,從要證明的不等式出發,尋找使這個不等式成立的某一"充分的"條件,為此逐步往前追溯(執果索因),一直追溯到已知條件或一些真命題為止.
根據題意可知, 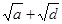 和
和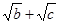 都是正數,所以為了證明結論,給不等式兩邊同時平方,而后根據題意
都是正數,所以為了證明結論,給不等式兩邊同時平方,而后根據題意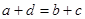 ,只需證明
,只需證明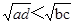 ,將其平方,可得
,將其平方,可得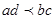 .由于不等式中含有四個未知數,所以可利用其中三個將另一個表示出來,不妨消掉
.由于不等式中含有四個未知數,所以可利用其中三個將另一個表示出來,不妨消掉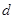 ,即
,即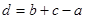 ,帶入
,帶入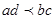 ,化簡可得
,化簡可得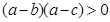 ,根據題意,
,根據題意,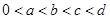 ,該不等式顯然成立.所以該不等式得證.
,該不等式顯然成立.所以該不等式得證.
試題解析:因為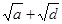 和
和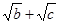 都是正數,
都是正數,
所以為了證明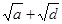 <
<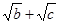
只需證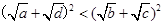
只需證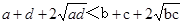
而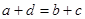
即證 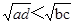
即證 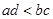
又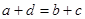 所以
所以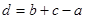
即證: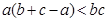
即證: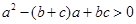
即證: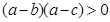
而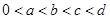
所以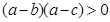 顯然成立
顯然成立
所以原不等式成立。
考點:分析法證明不等式.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com