
在如圖所示的幾何體中,四邊形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,點A,B,E,A1在一個平面內,AB=BC=CC1=2,AC=2 .
.

證明:(1)A1E∥AB.
(2)平面CC1FB⊥平面AA1EB.
見解析
【解析】【證明】(1)∵四邊形ACC1A1是矩形,
∴A1C1∥AC.又AC?平面ABC,A1C1?平面ABC,
∴A1C1∥平面ABC.
∵FC1∥BC,BC?平面ABC,∴FC1∥平面ABC.
又∵A1C1,FC1?平面A1EFC1,
∴平面A1EFC1∥平面ABC.
又∵平面ABEA1與平面A1EFC1、平面ABC的交線分別是A1E,AB,∴A1E∥AB.
(2)∵四邊形ACC1A1是矩形,∴AA1∥CC1.
∵∠BCC1=90°,即CC1⊥BC,∴AA1⊥BC.
又∵AB=BC=2,AC=2 ,∴AB2+BC2=AC2.
,∴AB2+BC2=AC2.
∴∠ABC=90°,即BC⊥AB.
∵AB,AA1?平面AA1EB,且AB∩AA1=A,
∴BC⊥平面AA1EB.
而BC?平面CC1FB,
∴平面CC1FB⊥平面AA1EB.


 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(九)第二章第六節練習卷(解析版) 題型:選擇題
已知冪函數f(x)的圖象過點P(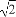 ,2),則f(5)等于( )
,2),則f(5)等于( )
(A)10 (B)16 (C)25 (D)32
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業(一)第一章第一節練習卷(解析版) 題型:選擇題
已知集合A={x|y=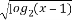 },B={y|y=
},B={y|y=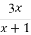 },則A∩B=( )
},則A∩B=( )
(A)[2,+∞) (B)[2,3)∪(3,+∞)
(C)(1,+∞) (D)[1,3)∪(3,+∞)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十四第七章第三節練習卷(解析版) 題型:填空題
如圖,在正方體ABCD-A1B1C1D1中,M,N分別是棱C1D1,C1C的中點.以下四個結論:

①直線AM與直線C1C相交;
②直線AM與直線BN平行;
③直線AM與直線DD1異面;
④直線BN與直線MB1異面.
其中正確結論的序號為 .(注:把你認為正確的結論序號都填上)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十六第七章第五節練習卷(解析版) 題型:解答題
如圖,A,B,C,D為空間四點.在△ABC中,AB=2,AC=BC= .等邊三角形ADB以AB為軸轉動.
.等邊三角形ADB以AB為軸轉動.

(1)當平面ADB⊥平面ABC時,求CD.
(2)當△ADB轉動時,是否總有AB⊥CD?證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十六第七章第五節練習卷(解析版) 題型:選擇題
已知直線m,n和平面α,β滿足m⊥n,m⊥α,α⊥β,則( )
(A)n⊥β (B)n∥β
(C)n⊥α (D)n∥α或n?α
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十八第七章第七節練習卷(解析版) 題型:解答題
如圖,在圓錐PO中,已知PO= ,☉O的直徑AB=2,C是
,☉O的直徑AB=2,C是 的中點,D為AC的中點.
的中點,D為AC的中點.

求證:平面POD⊥平面PAC.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十五第七章第四節練習卷(解析版) 題型:填空題
已知平面α∥平面β,P是α,β外一點,過點P的直線m分別與α,β交于A,C,過點P的直線n分別與α,β交于B,D,且PA=6,AC=9,PD=8,則BD的長為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十三第七章第二節練習卷(解析版) 題型:選擇題
已知某幾何體的三視圖如圖所示,其中俯視圖和側視圖都是腰長為4的等腰直角三角形,正視圖為直角梯形,則此幾何體的體積V的大小為( )
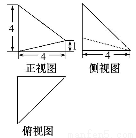
(A)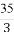 (B)12 (C)
(B)12 (C)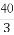 (D)16
(D)16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com