
已知函數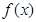 是二次函數,不等式
是二次函數,不等式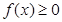 的解集為
的解集為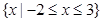 ,且
,且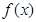 在區間
在區間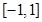 上的最小值是4.
上的最小值是4.
(Ⅰ)求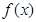 的解析式;
的解析式;
(Ⅱ)設 ,若對任意的
,若對任意的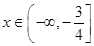 ,
, 均成立,求實數
均成立,求實數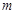 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:解答題
提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度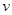 (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度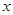 (單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當
(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0千米/小時;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當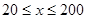 時,車流速度
時,車流速度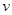 是車流密度
是車流密度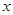 的一次函數.
的一次函數.
(Ⅰ)當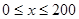 時,求函數
時,求函數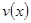 的表達式;
的表達式;
(Ⅱ)當車流密度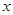 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)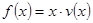 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲廠以x 千克/小時的速度運輸生產某種產品(生產條件要求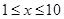 ),每小時可獲得利潤是
),每小時可獲得利潤是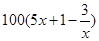 元.
元.
(1)要使生產該產品2小時獲得的利潤不低于3000元,求x的取值范圍;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)已知函數y=ln(-x2+x-a)的定義域為(-2,3),求實數a的取值范圍;
(2)已知函數y=ln(-x2+x-a)在(-2,3)上有意義,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數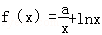 ,g(x)=
,g(x)=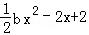 ,a,b∈R.
,a,b∈R.
(1)求函數f(x)的單調區間;
(2)記函數h(x)=f(x)+g(x),當a=0時,h(x)在(0,1)上有且只有一個極值點,求實數b的取值范圍;
(3)記函數F(x)=|f(x)|,證明:存在一條過原點的直線l與y=F(x)的圖象有兩個切點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com