
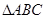 的頂點A(0,1),AB邊上的中線CD所在直線方程為
的頂點A(0,1),AB邊上的中線CD所在直線方程為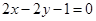 ,AC邊上的高BH所在直線方程為
,AC邊上的高BH所在直線方程為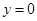 .
.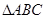 的項點B、C的坐標;
的項點B、C的坐標; ;(2)
;(2) .
. 在直線
在直線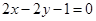 上,又
上,又 在
在 軸,即
軸,即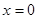 ,聯(lián)立可求
,聯(lián)立可求 ,又因為AC邊上的高BH所在直線方程為
,又因為AC邊上的高BH所在直線方程為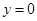 ,可得點
,可得點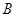 在
在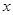 軸,設(shè)為
軸,設(shè)為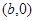 ,由
,由 是 邊
是 邊 的中點,根據(jù)中點坐標公式,把
的中點,根據(jù)中點坐標公式,把 的坐標用
的坐標用 表示出來,進而把
表示出來,進而把 的坐標代入直線
的坐標代入直線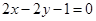 中,求
中,求 ;(2)弦的垂直平分線過圓心,故先求弦
;(2)弦的垂直平分線過圓心,故先求弦 的垂直平分線,再求弦
的垂直平分線,再求弦 垂直平分線,聯(lián)立求交點,即得圓心坐標,其中坐標都是用
垂直平分線,聯(lián)立求交點,即得圓心坐標,其中坐標都是用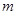 表示,再根據(jù)過圓心和切點的直線必與斜率為1的直線垂直,∴
表示,再根據(jù)過圓心和切點的直線必與斜率為1的直線垂直,∴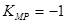 ,列式求
,列式求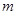 ,從而圓心確定,再根據(jù)兩點之間距離公式求半徑,圓的方程確定.
,從而圓心確定,再根據(jù)兩點之間距離公式求半徑,圓的方程確定.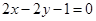 ,所以C(0, -
,所以C(0, - ) 2分
) 2分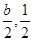 ),代入方程
),代入方程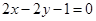
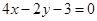
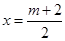 上. 設(shè)圓心M
上. 設(shè)圓心M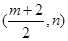
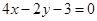 上,所以
上,所以 ①
① .
. ,整理得:
,整理得: ②
② 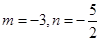 ,所以
,所以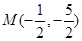 ,半徑
,半徑
 12分
12分

科目:高中數(shù)學 來源:不詳 題型:填空題
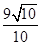 ,則直線L的方程為 (寫成直線的一般式).
,則直線L的方程為 (寫成直線的一般式).查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com