
數列 的前
的前 項和
項和 滿足
滿足 (
( ,且
,且 ).數列
).數列 滿足
滿足 .
.
(Ⅰ)求數列 的前
的前 項和
項和 ;
;
(Ⅱ)若對一切 都有
都有 ,求
,求 的取值范圍.
的取值范圍.
 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
(08年周至二中三模理) (12分)數列{![]() }的前
}的前![]() 項和
項和![]() 滿足:
滿足:![]() .
.
(1)求數列{![]() }的通項公式
}的通項公式![]() ;
;
(2)數列{![]() }中是否存在三項,它們可以構成等差數列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
}中是否存在三項,它們可以構成等差數列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分,(Ⅰ)問5分,(Ⅱ)問7分)
設![]() 個不全相等的正數
個不全相等的正數![]() 依次圍成一個圓圈.
依次圍成一個圓圈.
(Ⅰ)若![]() ,且
,且![]() 是公差為
是公差為![]() 的等差數列,而
的等差數列,而![]() 是公比為
是公比為![]() 的等比數列;數列
的等比數列;數列![]() 的前
的前![]() 項和
項和![]() 滿足:
滿足:![]() ,求通項
,求通項![]() ;
;
(Ⅱ)若每個數![]() 是其左右相鄰兩數平方的等比中項,求證:
是其左右相鄰兩數平方的等比中項,求證:![]() ;
; ![]()
![]()
查看答案和解析>>
科目:高中數學 來源:2015屆廣西桂林十八中高二上學期段考理科數學試卷(解析版) 題型:解答題
設數列 的前
的前 項和
項和 滿足
滿足 ,其中
,其中 .
.
⑴若 ,求
,求 及
及 ;
;
⑵若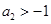 ,求證:
,求證: ,并給出等號成立的充要條件.
,并給出等號成立的充要條件.
查看答案和解析>>
科目:高中數學 來源:2013屆浙江桐鄉高級中學高二第二學期期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分15分)
已知各項均為正數的數列 中,數列的前
中,數列的前 項和
項和 滿足
滿足 .
.
(1)求 ;
;
(2)由(1)猜想數列 的通項公式,并用數學歸納法證明你的猜想.
的通項公式,并用數學歸納法證明你的猜想.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com