
某旅游推介活動晚會進行嘉賓現場抽獎活動,抽獎規則是:抽獎盒中裝有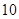 個大小相同的小球,分別印有“多彩十藝節”和“美麗泉城行”兩種標志,搖勻后,參加者每次從盒中同時抽取兩個小球,若抽到兩個球都印有“多彩十藝節”標志即可獲獎.
個大小相同的小球,分別印有“多彩十藝節”和“美麗泉城行”兩種標志,搖勻后,參加者每次從盒中同時抽取兩個小球,若抽到兩個球都印有“多彩十藝節”標志即可獲獎.
(I)活動開始后,一位參加者問:盒中有幾個“多彩十藝節”球?主持人笑說:我只知道從盒中同時抽兩球不都是“美麗泉城行”標志的概率是 ,求抽獎者獲獎的概率;
,求抽獎者獲獎的概率;
(Ⅱ)上面條件下,現有甲、乙、丙、丁四人依次抽獎,抽后放回,另一個人再抽,用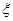 表示獲獎的人數,求
表示獲獎的人數,求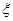 的分布列及
的分布列及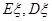 .
.
(I)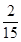 ;(Ⅱ)分布列如下解析;
;(Ⅱ)分布列如下解析;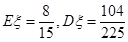 .
.
解析試題分析:(I)本題獲獎的標準是抽到兩個球都印有“多彩十藝節”標志即可獲獎.而所給的條件是兩球不都是“美麗泉城行”標志的概率是 ,不都是是都是的對立面.所以假設有n個標有“美麗泉城行”則都是“美麗泉城行”的概率為
,不都是是都是的對立面.所以假設有n個標有“美麗泉城行”則都是“美麗泉城行”的概率為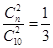 .計算出n的值.10-n就是印有“多彩十藝節”球的個數.即可求出抽獎者獲獎的概率.(Ⅱ)本小題是一個超幾何概型獨立性實驗.分布列和數學期望及方差公式.
.計算出n的值.10-n就是印有“多彩十藝節”球的個數.即可求出抽獎者獲獎的概率.(Ⅱ)本小題是一個超幾何概型獨立性實驗.分布列和數學期望及方差公式.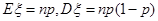 .本題主要是考查概率知識,由生活背景引出數學知識.數學知識學以致用.
.本題主要是考查概率知識,由生活背景引出數學知識.數學知識學以致用.
試題解析:(I)設印有“美麗泉城行”標志的球有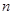 個,不都是“美麗泉城行”標志為事件
個,不都是“美麗泉城行”標志為事件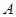 ,
,
則都是“美麗泉城行”標志的概率是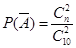 ,由對立事件的概率:
,由對立事件的概率: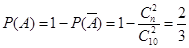 ,
,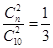
得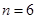 ,故“多彩十藝節”標志卡共有4張
,故“多彩十藝節”標志卡共有4張
∴抽獎者獲獎的概率為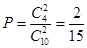 6分
6分
(Ⅱ)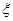 ~
~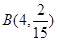 ,
,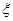 的分布列為
的分布列為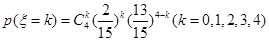 或
或
∴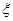
0 1 2 3 4 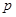
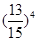
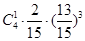
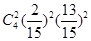
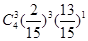
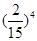
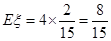
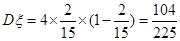 12分
12分
考點:1.概率的含義.2.對立事件.3.數學期望,數學方差的計算公式.4.獨立性檢驗知識點.


 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:高中數學 來源: 題型:解答題
為了參加廣州亞運會,從四支較強的排球隊中選出18人組成女子排球國家隊,隊員來源人數如下表:
| 對別 | 北京 | 上海 | 天津 | 八一 |
| 人數 | 4 | 6 | 3 | 5 |
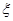 ,求隨機變量
,求隨機變量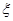 的分布列及數學期望
的分布列及數學期望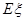
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個盒子裝有六張卡片,上面分別寫著如下六個定義域為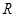 的函數:
的函數: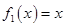 ,
, ,
,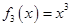 ,
,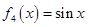 ,
,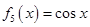 ,
,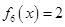 .
.
(1)現從盒子中任取兩張卡片,將卡片上的函數相加得一個新函數,求所得函數是奇函數的概率;
(2)現從盒子中進行逐一抽取卡片,且每次取出后均不放回,若取到一張記有偶函數的卡片則停止抽取,否則繼續進行,求抽取次數 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市為增強市民的環境保護意識,面向全市征召義務宣傳志愿者.把符合條件的1000名志愿者按年齡分組:第1組[20,25)、第2組[25,30)、第3組[30,35)、第4組[35,40)、第5組[40,45],得到的頻率分布直方圖如圖所示: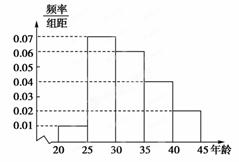
(1)若從第3、4、5組中用分層抽樣的方法抽取12名志愿者參加廣場的宣傳活動,應從第3、4、5組各抽取多少名志愿者?
(2)在(1)的條件下,該市決定在這12名志愿者中隨機抽取3名志愿者介紹宣傳經驗,求第4組至少有一名志愿者被抽中的概率;
(3)在(2)的條件下,若ξ表示抽出的3名志愿者中第3組的人數,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在一個盒子里裝有4枝圓珠筆,其中3枝一等品,1枝三等品
(1)從盒子里任取2枝恰有1枝三等品的概率多大?
(2)從盒子里第一次任取1枝(不放回),第二次任取1枝;第一次取的是三等品,第二次取的是一等品的概率有多大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某食品企業一個月內被消費者投訴的次數用 表示,椐統計,隨機變量
表示,椐統計,隨機變量 的概率分布如下:
的概率分布如下:
 | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 2a | a |
 的數學期望;
的數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品按質量標準分為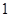 ,
, ,
,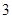 ,
,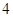 ,
,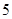 五個等級.現從一批該產品隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下:
五個等級.現從一批該產品隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下:
| 等級 | 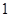 |  | 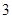 | 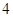 | 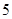 |
| 頻率 | 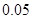 | 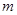 | 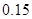 | 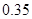 | 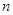 |
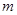 ,
, ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解甲、乙兩廠產品的質量,從兩廠生產的產品中分別隨機抽取各10件樣品,測量產品中某種元素的含量(單位:毫克).如圖是測量數據的莖葉圖: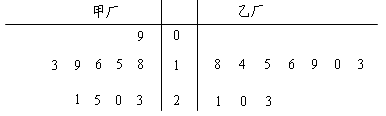
規定:當產品中的此種元素含量不小于18毫克時,該產品為優等品.
(1)試用上述樣本數據估計甲、乙兩廠生產的優等品率;
(2)從乙廠抽出的上述10件樣品中,隨機抽取3件,求抽到的3件樣品中優等品數 的分布列及其數學期望
的分布列及其數學期望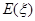 ;
;
(3)從甲廠的10件樣品中有放回的隨機抽取3件,也從乙廠的10件樣品中有放回的隨機抽取3件,求抽到的優等品數甲廠恰比乙廠多2件的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某次考試中,從甲,乙兩個班各抽取10名學生的成績進行統計分析,兩班10名學生成績的莖葉圖如圖所示,成績不小于90分為及格.
(1)從每班抽取的學生中各抽取一人,求至少有一個及格的概率;
(2)從甲班10人中取兩人,乙班10人中取一人,三人中及格人數記為X,求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com