中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

如圖，已知正三棱錐S-ABC，過B和側(cè)棱SA、SC的中點E、F作一截面，若這個截面與側(cè)面SAC垂直，求此三棱錐的側(cè)面積與底面積之比．
答案：略
解析：

解：取AC有中點M，連結(jié)SM．設SM∩EF=D．

在△SAC中，E、F分別為SA、SC的中點，

∴EF∥AC．

∴．而SF=FC，∴SD=DM．

∴D為SM的中點．

∵S-ABC為正三棱錐，∴△SAC為等腰三角形．

∴SM⊥AC．而AC∥EF，

∴SM⊥EF．又截面BEF⊥側(cè)面SAC．

∴SM⊥平面BEF．

∴SM⊥BD．又SD=DM．

∴△SBM為等腰三角形，∴SB=BM．

設正三棱錐S-ABC的底面邊長為a，則，

從而SA=SB=SC=BM=．

又，

∴

∴．

通過截面與側(cè)面垂直，尋找斜高與底面邊長的關系，找出二者的關系后，問題就可解決．


練習冊系列答案
相關習題

科目：高中數(shù)學 來源： 題型：

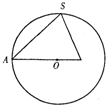已知正三棱錐S-ABC內(nèi)接于半徑為6的球，過側(cè)棱SA及球心O的平面截三棱錐及球面所得截面如右圖，則此三棱錐的側(cè)面積為
27
15
27
15
．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：044

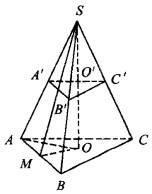
已知正三棱錐S-ABC的高SO=h，斜高SM=l，求經(jīng)過SO的中點O′平行于底面的截面△A′B′C′的面積(如圖所示)．

v

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：044

如圖，已知正三棱錐S-ABC，過B和側(cè)棱SA、SC的中點E、F作一截面，若這個截面與側(cè)面SAC垂直，求此三棱錐的側(cè)面積與底面積之比．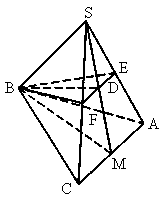

查看答案和解析>>

科目：高中數(shù)學 來源：2010年陜西省咸陽市禮泉一中高三5月最后一次預測數(shù)學試卷（解析版） 題型：解答題

已知正三棱錐S-ABC內(nèi)接于半徑為6的球，過側(cè)棱SA及球心O的平面截三棱錐及球面所得截面如右圖，則此三棱錐的側(cè)面積為    ．

查看答案和解析>>

同步練習冊答案