已知二次函數f(x)滿足f(2)＝－1,f(－1)＝－1，且f(x)的最大值為8，求二次函數f(x)的解析式．
f(x)＝－4x2＋4x＋7
【解析】(解法1：利用一般式)設f(x)＝ax2＋bx＋c(a≠0)，
解得
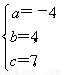
∴所求二次函數為f(x)＝－4x2＋4x＋7.
(解法2：利用頂點式)設f(x)＝a(x－m)2＋n，∵f(2)＝f(－1)，∴拋物線對稱軸為x＝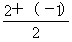
＝
，即m＝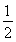
；又根據題意，函數最大值ymax＝8，
∴n＝8，∴f(x)＝a
2＋8.∵f(2)＝－1，∴a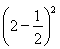
＋8＝－1，解得a＝－4.
∴f(x)＝－42＋8＝－4x2＋4x＋7.
(解法3：利用兩根式)由題意知f(x)＋1＝0的兩根為x1＝2，x2＝－1，故可設f(x)＋1＝a(x－2)(x＋1)，即f(x)＝ax2－ax－2a－1.又函數有最大值ymax＝8，即
＝8，解得a＝－4或a＝0(舍)，∴所求函數的解析式為f(x)＝－4x2－(－4)x－2×(－4)－1＝－4x2＋4x＋7
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷（解析版） 題型：填空題
若數列{an}的前n項和Sn＝n2＋3n，則a6＋a7＋a8＝________．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第7課時練習卷（解析版） 題型：填空題
已知三數x＋log272，x＋log92，x＋log32成等比數列，則公比為________．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第6課時練習卷（解析版） 題型：填空題
設函數f(x)＝x2－1，對任意x∈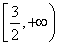
，f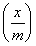
－4m2f(x)≤f(x－1)＋4f(m)恒成立，則實數m的取值范圍是________．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第6課時練習卷（解析版） 題型：解答題
已知函數f(x)＝x2＋mx＋n的圖象過點(1，3)，且f(－1＋x)＝f(－1－x)對任意實數都成立，函數y＝g(x)與y＝f(x)的圖象關于原點對稱．
(1)求f(x)與g(x)的解析式；
(2)若F(x)＝g(x)－λf(x)在(－1，1]上是增函數，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第5課時練習卷（解析版） 題型：填空題
設函數f(x)(x∈R)滿足f(－x)＝f(x)，f(x)＝f(2－x)，且當x∈[0，1]時f(x)＝x3.又函數g(x)＝|xcos(πx)|，則函數h(x)＝g(x)－f(x)在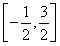
上的零點個數為________．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第5課時練習卷（解析版） 題型：解答題
當m為何值時，方程x2－4|x|＋5－m＝0有四個不相等的實數根？
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第4課時練習卷（解析版） 題型：解答題
已知定義在R上的函數f(x)對任意實數x、y恒有f(x)＋f(y)＝f(x＋y)，且當x＞0時，f(x)＜0，又f(1)＝－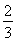
.
(1)求證：f(x)為奇函數；
(2)求證：f(x)在R上是減函數；
(3)求f(x)在[－3，6]上的最大值與最小值．
查看答案和解析>>
科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第2課時練習卷（解析版） 題型：解答題
求下列函數的值域：
(1) y＝x－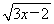
；
(2) y＝x2－2x－3，x∈(－1，4]；
(3) y＝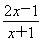
，x∈[3，5]；
(4) y＝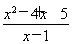
(x>1)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com