在直角坐標(biāo)系xOy中,已知向量
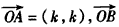
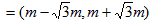
,其中k>0,m>0。
(Ⅰ)當(dāng)m=k=1時,證明
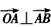
;
(Ⅱ)求向量
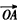
和
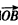
夾角的大小;
(Ⅲ)設(shè)
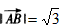
,求
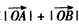
的最大值。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
在直角坐標(biāo)系xOy中,橢圓C
1:
+=1(a>b>0)的左、右焦點(diǎn)分別為F
1,F(xiàn)
2.F
2也是拋物線C
2:y
2=4x的焦點(diǎn),點(diǎn)M為C
1與C
2在第一象限的交點(diǎn),且|MF
2|=
.
(Ⅰ)求C
1的方程;
(Ⅱ)平面上的點(diǎn)N滿足
=+,直線l∥MN,且與C
1交于A,B兩點(diǎn),若
•=0,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在直角坐標(biāo)系xOy中,已知點(diǎn)P(2cosx+1,2cos2x+2)和點(diǎn)Q(cosx,-1),其中x∈[0,π].若向量
與
垂直,求x的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:

如圖所示,在直角坐標(biāo)系xOy中,射線OA在第一象限,且與x軸的正半軸成定角60°,動點(diǎn)P在射線OA上運(yùn)動,動點(diǎn)Q在y軸的正半軸上運(yùn)動,△POQ的面積為
2.
(1)求線段PQ中點(diǎn)M的軌跡C的方程;
(2)R
1,R
2是曲線C上的動點(diǎn),R
1,R
2到y(tǒng)軸的距離之和為1,設(shè)u為R
1,R
2到x軸的距離之積.問:是否存在最大的常數(shù)m,使u≥m恒成立?若存在,求出這個m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在直角坐標(biāo)系xOy中,已知圓M的方程為x
2+y
2-4xcosα-2ysinα+3cos
2α=0(α為參數(shù)),直線l的參數(shù)方程為
(t為參數(shù))
(I)求圓M的圓心的軌跡C的參數(shù)方程,并說明它表示什么曲線;
(II)求直線l被軌跡C截得的最大弦長.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在直角坐標(biāo)系xOy中,已知橢圓
C:+=1(a>b>0)的離心率e=
,左右兩個焦分別為F
1,F(xiàn)
2.過右焦點(diǎn)F
2且與x軸垂直的直線與橢圓C相交M、N兩點(diǎn),且|MN|=2.
(1)求橢圓C的方程;
(2)設(shè)橢圓C的一個頂點(diǎn)為B(0,-b),是否存在直線l:y=x+m,使點(diǎn)B關(guān)于直線l 的對稱點(diǎn)落在橢圓C上,若存在,求出直線l的方程,若不存在,請說明理由.
查看答案和解析>>

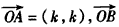
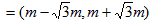 ,其中k>0,m>0。
,其中k>0,m>0。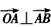 ;
;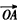 和
和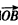 夾角的大小;
夾角的大小;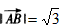 ,求
,求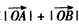 的最大值。
的最大值。 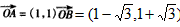 ,
,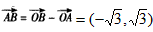 ,
,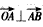 ;
;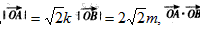 =2km,設(shè)向量
=2km,設(shè)向量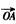 和
和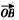 的夾角為θ,
的夾角為θ,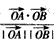 =
=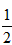 ,
,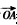 和
和 的夾角等于
的夾角等于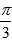 ;
;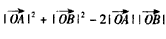
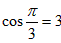 ,
,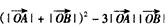
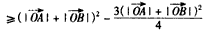
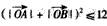 ,
,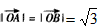 時,等號成立,所以
時,等號成立,所以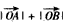 的最大值為
的最大值為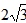 。
。


 如圖所示,在直角坐標(biāo)系xOy中,射線OA在第一象限,且與x軸的正半軸成定角60°,動點(diǎn)P在射線OA上運(yùn)動,動點(diǎn)Q在y軸的正半軸上運(yùn)動,△POQ的面積為2
如圖所示,在直角坐標(biāo)系xOy中,射線OA在第一象限,且與x軸的正半軸成定角60°,動點(diǎn)P在射線OA上運(yùn)動,動點(diǎn)Q在y軸的正半軸上運(yùn)動,△POQ的面積為2