已知向量m＝(sinA，cosA)，n＝(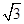
，－1)，m·n＝1，且A為銳角．
(1)求角A的大小；
(2)求函數f(x)＝cos2x＋4cosAsinx(x∈R)的值域．
(1)A＝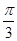
.(2)函數f(x)的值域是
.
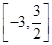【解析】
試題分析：(1)由題意得m·n＝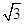
sinA－cosA＝1，
2sin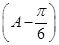
＝1，sin＝
，
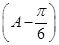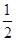由A為銳角得，A－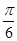
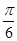＝，∴A＝.
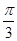(2)由(1)知cosA＝，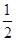
所以f(x)＝cos2x＋2sinx＝1－2sin2x＋2sinx
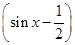＝－2
2＋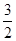
.
因為x∈R，所以sinx∈[－1,1]，
因此，當sinx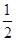＝時，f(x)有最大值，
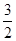當sinx＝－1時，f(x)有最小值－3，
所以所求函數f(x)的值域是.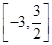
考點：平面向量的坐標運算，和差倍半的三角函數，三角函數的圖象和性質，二次函數的圖象和性質。
點評：中檔題，本題較為典型，即首先通過平面向量的坐標運算，得到三角函數式，利用和差倍半的三角函數公式，將三角函數式“化一”，進一步研究函數的圖像和性質。本題利用換元思想，將問題轉化成二次函數在閉區間的最值問題，使問題更具綜合性。
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目：高中數學 來源：2011屆高考數學第一輪復習測試題6 題型：044
(理)已知向量m＝(sinωx＋cosωx，
cosωx)，n＝(cosωx－sinωx，2 sinωx)，其中ω＞0，函數f(x)＝m·n，若f(x)相鄰兩對稱軸間的距離為
．
(1)求ω的值，并求f(x)的最大值及相應x的集合；
(2)在△ABC中，a、b、c分別是A、B、C所對的邊，△ABC的面積S＝5
，b＝4，f(A)＝1，求邊a的長．
查看答案和解析>>
科目：高中數學 來源：江西省臨川一中、新余四中2012屆高三上學期期中考試數學文科試題 題型：044
已知向量m＝(
sin
，1)，n＝(cos，cos2)，f(x)＝m·n．
(1)若f(x)＝1，求cos(x＋
)的值；
(2)在△ABC中，角A，B，C的對邊分別是a，b，c且滿足acosC＋
c＝b，求函數f(B)的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2010-2011學年湖南省長沙市高三第六次月考理科數學卷 題型：解答題
(本小題滿分12分)
已知向量m＝(sin，1)，n＝(cos，cos2)，f(x)＝m·n.
(1)若f(x)＝1，求cos(－x)的值；
(2)在△ABC中，角A，B，C的對邊分別是a，b，c且滿足acosC＋c＝b，求函數f(B)的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
已知向量m＝(
sin
，1)，n＝(cos，cos2)，f(x)＝m·n.
(1)若f(x)＝1，求cos(x＋
)的值；
(2)在△ABC中，角A，B，C的對邊分別是a，b，c且滿足acosC＋
c＝b，求函數f(B)的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
已知向量m＝(
sin
，1)，n＝(cos，cos2)．
(1)若m·n＝1，求cos(
－x)的值；
(2)記f(x)＝m·n，在△ABC中，角A，B，C的對邊分別是a，b，c，且滿足(2a－c)cosB＝bcosC，求函數f(A)的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com