
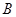 為鈍角的的三角形
為鈍角的的三角形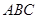 內角
內角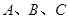 的對邊分別為
的對邊分別為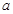 、
、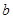 、
、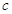 ,
,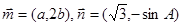 ,且
,且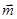 與
與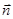 垂直.
垂直.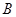 的大小;
的大小;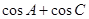 的取值范圍
的取值范圍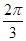 ;(2)
;(2)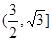 .
.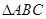 的邊角之間的關系,題中只有
的邊角之間的關系,題中只有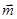 與
與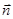 垂直提供的等量關系是
垂直提供的等量關系是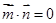 ,即
,即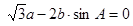 ,這正是我們需要的邊角關系.因為要求角
,這正是我們需要的邊角關系.因為要求角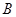 ,故把等式中的邊化為角,我們用正弦定理,
,故把等式中的邊化為角,我們用正弦定理,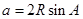 ,
,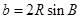 ,代入上述等式得
,代入上述等式得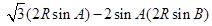
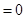 ,得出
,得出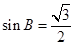 ,從而可求出角
,從而可求出角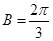 ;(2)要求
;(2)要求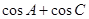 的范圍,式子中有兩個角不太好計算,可以先把兩個角化為一個角,由(1)
的范圍,式子中有兩個角不太好計算,可以先把兩個角化為一個角,由(1)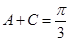 ,從而
,從而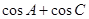
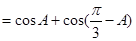 ,再所其化為一個三角函數(這是解三角函數問題常用方法),下面只要注意
,再所其化為一個三角函數(這是解三角函數問題常用方法),下面只要注意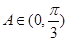 這個范圍即可.
這個范圍即可. 垂直
垂直 ,∴
,∴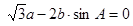 (2分)
(2分)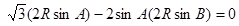 (4分)
(4分)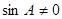 ,∴
,∴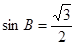 ,(6分) 又∵∠B是鈍角,∴∠B
,(6分) 又∵∠B是鈍角,∴∠B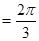 (7分)
(7分) 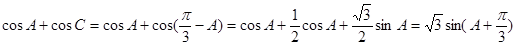 (3分)
(3分)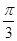 ),
),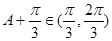 , (4分)
, (4分)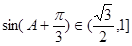 ,(6分) ∴
,(6分) ∴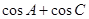 的取值范圍是
的取值范圍是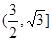 (7分)
(7分)

 習題精選系列答案
習題精選系列答案科目:高中數學 來源:不詳 題型:解答題
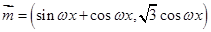 ,
,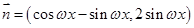 ,其中
,其中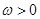 ,若函數
,若函數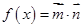 ,且函數
,且函數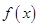 的圖象與直線y=2兩相鄰公共點間的距離為
的圖象與直線y=2兩相鄰公共點間的距離為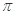 .
.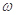 的值;
的值;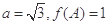 ,求△ABC周長的取值范圍.
,求△ABC周長的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
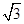 ).
).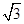 f
f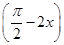 -2f2(x)在區間
-2f2(x)在區間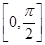 上的值域.
上的值域.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com