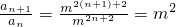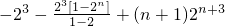解:(1)由題意f(a
n)=4+2(n-1)=2n+2,
即log
ma
n=2n+2
∴a
n=m
2n+2∴
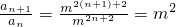
∵m>0且m≠1,∴m
2為非零常數,
∴數列{a
n}是以m
4為首項,m
2為公比的等比數列
(2)由題意b
n=a
nf(a
n)=m
2n+2log
mm
2n+2=(2n+2)•m
2n+2,
當

∴S
n=2•2
3+3•2
4+4•2
5+…+(n+1)•2
n+2①
①式兩端同乘以2,得2S
n=2•2
4+3•2
5+4•2
6+…+n•2
n+2+(n+1)•2
n+3②
②-①并整理,得S
n=-2•2
3-2
4-2
5-2
6-…-2
n+2+(n+1)•2
n+3
=-2
3-[2
3+2
4+2
5+…+2
n+2]+(n+1)•2
n+3=
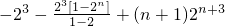
=-2
3+2
3(1-2
n)+(n+1)•2
n+3=2
n+3•n
分析:(1)利用等差數列的通項公式求出f(a
n),利用對數的定義求出a
n,求出相鄰兩項的比,利用等比數列的定義得證.
(2)求出b
n,將m的值代入,利用錯位相減法求出數列的前n項和S
n.
點評:要證明一個數列是等差數列(等比數列)一般利用兩個特殊數列的定義;求數列的前n項和,首先判斷數列的通項的特點,再選擇合適的方法.

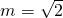 時,求Sn.
時,求Sn.