解:(I)當|x|<2時,由

⊥

得

得(x
2-3)x-y=0,y=x
3-3x(|x|<2且x≠0);
當|x|≥2時,由

,得y=-
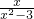
,
∴y=f(x)=
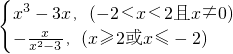
(II)對?x∈(-∞,-2]∪[2,+∞),都有mx
2+x-3m≥0即m(x
2-3)≥-x,
也就是m≥

對?x∈(-∞,-2]∪[2,+∞)恒成立,
由(2)知當|x|≥2時,f′(x)=
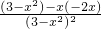
=

>0
∴函數f(x)在(-∞,-2]和[2,+∞)都單調遞增
又f(-2)=
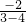
=2,f(2)=-2
當x≤-2時f(x)=

>0,
∴當x∈(-∞,-2]時,0<f(x)≤2同理可得,當x≥2時,有-2≤f(x)<0,
綜上所述得,對x∈(-∞,-2]∪[2,+∞),f(x)取得最大值2;
∴實數m的取值范圍為m≥2.
分析:(I)因為當|x|<2時,

⊥

得

得到y與x的關系式;當|x|≥2時,

,得到 y與x的另一關系式,聯立得到f(x)為分段函數;
(II)根據mx
2+x-3m≥0解出m≥

,分區間討論x的范圍得到f(x)的最大值,讓m大于等于最大值即可求出m的范圍.
點評:考查學生利用導數研究函數單調性的能力,學會用數量積判斷兩個向量的垂直關系,理解平行向量及共線向量滿足的條件,熟悉分段函數的解析式,理解函數恒成立時所取的條件.

 =(x2-3,1),
=(x2-3,1), =(x,-y)(其中實數x和y不同時為零),當|x|<2時,有
=(x,-y)(其中實數x和y不同時為零),當|x|<2時,有 ⊥
⊥ ,當|x|≥2時,
,當|x|≥2時, ∥
∥ .
. ⊥
⊥ 得
得 得(x2-3)x-y=0,y=x3-3x(|x|<2且x≠0);
得(x2-3)x-y=0,y=x3-3x(|x|<2且x≠0); ,得y=-
,得y=-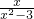 ,
,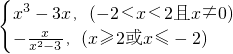
 對?x∈(-∞,-2]∪[2,+∞)恒成立,
對?x∈(-∞,-2]∪[2,+∞)恒成立,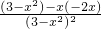 =
= >0
>0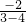 =2,f(2)=-2
=2,f(2)=-2 >0,
>0, ⊥
⊥ 得
得  得到y與x的關系式;當|x|≥2時,
得到y與x的關系式;當|x|≥2時, ,得到 y與x的另一關系式,聯立得到f(x)為分段函數;
,得到 y與x的另一關系式,聯立得到f(x)為分段函數; ,分區間討論x的范圍得到f(x)的最大值,讓m大于等于最大值即可求出m的范圍.
,分區間討論x的范圍得到f(x)的最大值,讓m大于等于最大值即可求出m的范圍.

 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案