
設甲、乙、丙三人每次射擊命中目標的概率分別為0.7、0.6和0.5.三人各向目標射擊一次,求至少有一人命中目標的概率及恰有兩人命中目標的概率.
0.94 0.44
解析解:設Ak表示“第k人命中目標”,k=1,2,3.
這里,A1,A2,A3獨立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
從而,至少有一人命中目標的概率為1-P( 1·
1· 2·
2· 3)=1-P(
3)=1-P( 1)P(
1)P( 2)P(
2)P( 3)=1-0.3×0.4×0.5=0.94.
3)=1-0.3×0.4×0.5=0.94.
恰有兩人命中目標的概率為
P(A1·A2· 3+A1·
3+A1· 2·A3+
2·A3+ 1·A2·A3)
1·A2·A3)
=P(A1·A2· 3)+P(A1·
3)+P(A1· 2·A3)+P(
2·A3)+P( 1·A2·A3)
1·A2·A3)
=P(A1)P(A2)P( 3)+P(A1)P(
3)+P(A1)P( 2)P(A3)+
2)P(A3)+
P( 1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
∴至少有一人命中目標的概率為0.94,恰有兩人命中目標的概率為0.44.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:解答題
有驅蟲藥1618和1573各3杯,從中隨機取出3杯稱為一次試驗(假定每杯被取到的概率相等),將1618全部取出稱為試驗成功.
(1)求恰好在第3次試驗成功的概率(要求將結果化為最簡分數).
(2)若試驗成功的期望值是2,需要進行多少次相互獨立重復試驗?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩藥廠生產同一型號藥品,在某次質量檢測中,兩廠各有5份樣品送檢,檢測的平均得分相等(檢測滿分為100分,得分高低反映該樣品綜合質量的高低).成績統計用莖葉圖表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
 ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
據IEC(國際電工委員會)調查顯示,小型風力發電項目投資較少,且開發前景廣闊,但受風力自然資源影響,項目投資存在一定風險.根據測算,風能風區分類標準如下:
假設投資A項目的資金為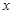 (
( ≥0)萬元,投資B項目資金為
≥0)萬元,投資B項目資金為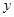 (
(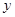 ≥0)萬元,調研結果是:未來一年內,位于一類風區的A項目獲利
≥0)萬元,調研結果是:未來一年內,位于一類風區的A項目獲利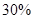 的可能性為
的可能性為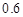 ,虧損
,虧損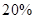 的可能性為
的可能性為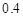 ;位于二類風區的B項目獲利
;位于二類風區的B項目獲利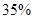 的可能性為
的可能性為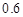 ,虧損
,虧損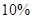 的可能性是
的可能性是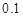 ,不賠不賺的可能性是
,不賠不賺的可能性是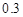 .
.
(1)記投資A,B項目的利潤分別為 和
和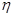 ,試寫出隨機變量
,試寫出隨機變量 與
與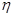 的分布列和期望
的分布列和期望 ,
,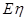 ;
;
(2)某公司計劃用不超過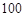 萬元的資金投資于A,B項目,且公司要求對A項目的投
萬元的資金投資于A,B項目,且公司要求對A項目的投
資不得低于B項目,根據(1)的條件和市場調研,試估計一年后兩個項目的平均利
潤之和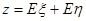 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對一批共50件的某電器進行分類檢測,其重量(克)統計如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件數 | 5 | a | 15 | b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某批產品中,有放回地抽取產品二次,每次隨機抽取1件,假設事件A“取出的2件產品都是二等品”的概率P(A)=0.04
(1)求從該批產品中任取1件是二等品的概率;
(2)若該批產品共10件,從中任意抽取2件;X表示取出的2件產品中二等品的件數,求X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個袋中裝有若干個大小相同的黑球、白球和紅球,已知從袋中任意摸出1個球,得到黑球的概率是 ;從袋中任意摸出2個球,至少得到1個白球的概率是
;從袋中任意摸出2個球,至少得到1個白球的概率是 .
.
(1)若袋中共有10個球,
①求白球的個數;
②從袋中任意摸出3個球,記得到白球的個數為X,求隨機變量X的分布列.
(2)求證:從袋中任意摸出2個球,至少得到1個黑球的概率不大于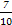 ,并指出袋中哪種顏色的球的個數最少.
,并指出袋中哪種顏色的球的個數最少.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在添加劑的搭配使用中,為了找到最佳的搭配方案,需要對各種不同的搭配方式作比較.在試制某種洗滌劑時,需要選用兩種不同的添加劑.現有芳香度分別為1,2,3,4,5,6的六種添加劑可供選用.根據試驗設計原理,通常首先要隨機選取兩種不同的添加劑進行搭配試驗.用X表示所選用的兩種不同的添加劑的芳香度之和.求所選用的兩種不同的添加劑的芳香度之和等于6的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com