在(3x-2y)20的展開式中,
求:(1)二項式系數最大的項;
(2)系數絕對值最大的項;
(3)系數最大的項.
【答案】
分析:(1)利用展開式中中間項的二項式系數最大,判斷出第11項的二項式系數最大;利用二項展開式的通項公式求出第11項.
(2)根據最大的系數絕對值大于等于其前一個系數絕對值;同時大于等于其后一個系數絕對值;列出不等式求出系數絕對值最大的項.
(3)據系數正負交替出現,故求系數最大的項,只需研究奇數項的系數即可;據最大的系數大于等于其前一個系數同時大于等于其后一個系數;列出不等式求出系數最大的項.
解答:解:(1)二項式系數最大的項是第11項,
T
11=C
20103
10(-2)
10x
10y
10=C
20106
10x
10y
10.
(2)設系數絕對值最大的項是第k+1項,于是
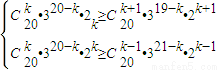
,
化簡得
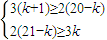
,
解得7
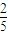
≤k≤8
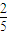
.
所以k=8,即T
9=C
2083
12•2
8•x
12y
8是系數絕對值最大的項.
(3)由于系數為正的項為奇數項,故可設第2k-1項系數最大,于是
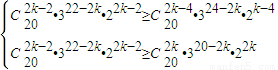
,
化簡得
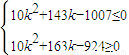
.
又k為不超過11的正整數,可得k=5,即第2×5-1=9項系數最大,T
9=C
208•3
12•2
8•x
12•y
8.
點評:本題考查二項式系數的性質:中間項的二項式系數最大、考查二項展開式的通項公式、考查求系數最大項的方法.

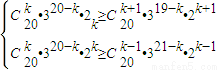 ,
,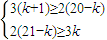 ,
,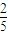 ≤k≤8
≤k≤8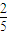 .
.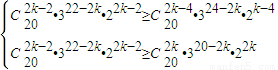 ,
,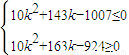 .
.

 選做題(在A、B、C、D四小題中只能選做兩題,并將選作標記用2B鉛筆涂黑,每小題10分,共20分,請在答題指定區域內作答,解答時應寫出文字說明、證明過程或演算步驟).
選做題(在A、B、C、D四小題中只能選做兩題,并將選作標記用2B鉛筆涂黑,每小題10分,共20分,請在答題指定區域內作答,解答時應寫出文字說明、證明過程或演算步驟).