Question

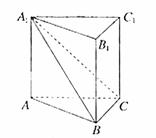
（湖北卷理18）如圖，在直三棱柱中，平面側面.

（Ⅰ）求證：；

（Ⅱ）若直線與平面所成的角為,二面角的大小為，試判斷與的大小關系，并予以證明.

Answer 1

解：本小題主要考查直棱柱、直線與平面所成角、二面角和線面關系等有關知識，同時考查空間想象能力和推理能力.（滿分12分）

（Ⅰ）證明：如右圖，過點A在平面A₁ABB₁內作

AD⊥A₁B于D，則

由平面A₁BC⊥側面A₁ABB₁,且平面A₁BC側面A₁ABB₁=A₁B,得

AD⊥平面A₁BC,又BC平面A₁BC，

所以AD⊥BC.

因為三棱柱ABC—A₁B₁C₁是直三棱柱，則AA₁⊥底面ABC，所以AA₁⊥BC.

又AA₁AD=A,從而BC⊥側面A₁ABB₁，又AB側面A₁ABB₁，故AB⊥BC.

（Ⅱ）解法1：連接CD，則由（Ⅰ）知是直線AC與平面A₁BC所成的角，

是二面角A₁—BC—A的平面角，即

于是在Rt△ADC中，在Rt△ADB中，

由AB＜AC，得又所以

解法2：由（Ⅰ）知，以點B為坐標原點，以BC、BA、BB₁所在的直線分

別為x軸、y軸、z軸，建立如圖所示的空間直角坐標系，設AA₁=a,AC=b,

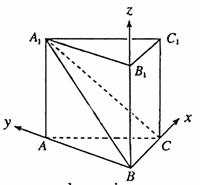AB=c,則 B(0,0,0), A(0,c,0), 于是

設平面A₁BC的一個法向量為n=(x,y,z)，則

由得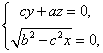

可取n=(0,-a,c)，于是與n的夾角為銳角，則與互為余角.

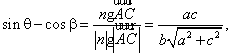
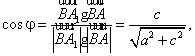所以

于是由c＜b，得

即又所以