
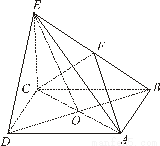
在四棱錐 中,底面
中,底面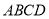 是正方形,
是正方形,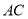 與
與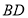 交于點
交于點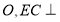 底面
底面 ,
, 為
為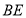 的中點.
的中點.
(1)求證: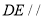 平面
平面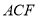 ;
;
(2)若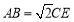 ,在線段
,在線段 上是否存在點
上是否存在點 ,使
,使 平面
平面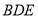 ?若存在,求出
?若存在,求出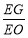 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(1)詳見解析;(2)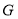 為線段
為線段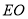 的中點時,
的中點時,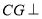 平面
平面 ,理由詳見解析.
,理由詳見解析.
【解析】
試題分析:(1)利用三角形的中位線定理證明 ,然后根據線面平行的判定定理進行證明即可;(2)這是存在性問題,先假設存在點
,然后根據線面平行的判定定理進行證明即可;(2)這是存在性問題,先假設存在點 ,使得
,使得 平面
平面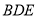 ,依據面面垂直的判定定理可知,這時必有面
,依據面面垂直的判定定理可知,這時必有面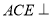 面
面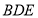 ,此時應該在平面
,此時應該在平面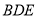 中可以找到一條直線垂直平面
中可以找到一條直線垂直平面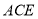 ,這時關注好題目中的條件:底面
,這時關注好題目中的條件:底面 為正方形且
為正方形且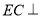 面
面 ,此時可想到可能是
,此時可想到可能是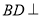 面
面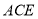 ,這個垂直關系并不難證明,故可肯定點
,這個垂直關系并不難證明,故可肯定點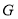 是存在的,然后再根據題中所給的條件去確定邊
是存在的,然后再根據題中所給的條件去確定邊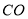 與
與 的比例關系,最后根據
的比例關系,最后根據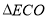 為直角三角形且
為直角三角形且 可確定
可確定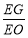 的比值.
的比值.
試題解析:(1)證明:連接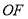
由四邊形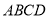 是正方形可知,點
是正方形可知,點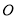 為
為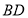 的中點
的中點
又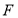 為
為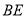 的中點,所以
的中點,所以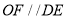
又 平面
平面 ,
,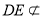 平面
平面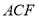
所以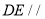 平面
平面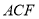 6分
6分
(2)解法一:若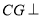 平面
平面 ,則必有
,則必有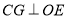
于是作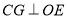 于點
于點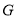
由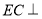 底面
底面 ,所以
,所以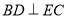 ,又底面
,又底面 是正方形
是正方形
所以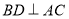 ,又
,又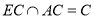 ,所以
,所以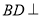 平面
平面 10分
10分
而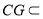 平面
平面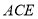 ,所以
,所以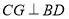
又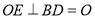 ,所以
,所以 平面
平面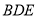 12分
12分
又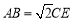 ,所以
,所以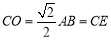
所以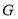 為
為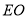 的中點,所以
的中點,所以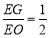 14分
14分
解法二:取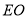 的中點
的中點 ,連接
,連接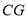 ,在四棱錐
,在四棱錐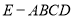 中
中
 ,
,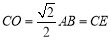 ,所以
,所以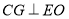 6分
6分
又由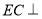 底面
底面 ,
,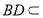 底面
底面 ,所以
,所以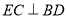
由四邊形 是正方形可知,
是正方形可知,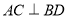
又
所以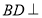 平面
平面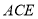 10分
10分
而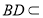 平面
平面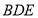
所以,平面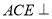 平面
平面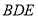 ,且平面
,且平面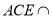 平面
平面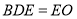
因為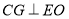 ,
,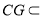 平面
平面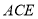 ,所以
,所以 平面
平面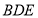 12分
12分
故在線段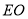 上存在點
上存在點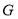 ,使
,使 平面
平面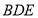
由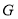 為
為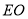 的中點,得
的中點,得 14分.
14分.
考點:1.空間中的平行關系;2.空間中的垂直關系.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源:2015屆安徽蚌埠高二第一學期期末考試文科數學試卷(解析版) 題型:選擇題
如圖是計算函數 的值的程序框圖,在①、②、③處應分別填入的是( )
的值的程序框圖,在①、②、③處應分別填入的是( )
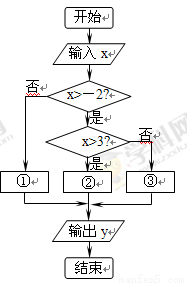
A.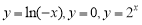 B.
B.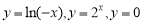
C. 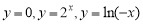 D.
D.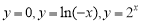
查看答案和解析>>
科目:高中數學 來源:2015屆四川資陽市高二第一學期期末考試理科數學試卷(解析版) 題型:填空題
在邊長為3的正方形 內任取一點
內任取一點 ,則
,則 到正方形四邊的距離均不小于l的概率為_______________.
到正方形四邊的距離均不小于l的概率為_______________.
查看答案和解析>>
科目:高中數學 來源:2015屆四川資陽市高二第一學期期末考試理科數學試卷(解析版) 題型:選擇題
從集合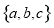 的所有子集中任取一個,這個集合恰是集合
的所有子集中任取一個,這個集合恰是集合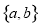 的子集的概率是( )
的子集的概率是( )
A.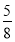 B.
B.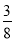 C.
C.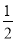 D.
D.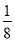
查看答案和解析>>
科目:高中數學 來源:2015屆四川資陽市高二第一學期期末考試文科數學試卷(解析版) 題型:解答題
在一個花瓶中裝有6枝鮮花,其中3枝山茶花,2枝杜鵑花和1枝君子蘭,從中任取2枝鮮花.
(1)求恰有一枝山茶花的概率;
(2)求沒有君子蘭的概率.
查看答案和解析>>
科目:高中數學 來源:2015屆吉林省吉林市高二上學期期末理數學試卷(解析版) 題型:填空題
已知F1,F2是橢圓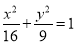 的兩焦點,過點F2的直線交橢圓于A,B兩點.在
的兩焦點,過點F2的直線交橢圓于A,B兩點.在
△AF1B中,若有兩邊之和是10,則第三邊的長度為
查看答案和解析>>
科目:高中數學 來源:2015屆北京海淀區高二上學期期末考試理科數學試卷(解析版) 題型:填空題
如圖所示,已知點 是正方體
是正方體 的棱
的棱 上的一個動點,設異面直線
上的一個動點,設異面直線 與
與 所成的角為
所成的角為 ,則
,則 的最小值是 .
的最小值是 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com