
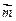 =(1+cosB,sinB)且與向量
=(1+cosB,sinB)且與向量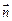 =(0,1)所成的角為
=(0,1)所成的角為 ,其中A、B、C為ΔABC的三個內角。
,其中A、B、C為ΔABC的三個內角。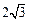 ,求ΔABC周長的最大值。
,求ΔABC周長的最大值。 。(2)ΔABC的周長的最大值為
。(2)ΔABC的周長的最大值為 。
。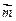 =(1+cosB,sinB)與
=(1+cosB,sinB)與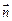 =(0,1)所成的角為
=(0,1)所成的角為
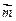 與向量
與向量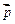 =(1,0)所成的角為
=(1,0)所成的角為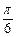
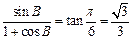 ,即
,即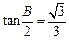 (2分)
(2分)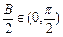 ,∴
,∴ ,∴B=
,∴B= 。 (4分)
。 (4分) ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac=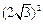 ,∵a,c>0。 (6分)
,∵a,c>0。 (6分)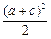 ,ac≤
,ac≤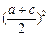 (當且僅當a=c時等號成立)
(當且僅當a=c時等號成立)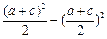
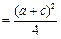 (8分)
(8分)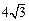 ,∴a+b+c≤
,∴a+b+c≤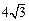 +
+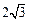 =
= (當且僅當a=c時取等號)
(當且僅當a=c時取等號) 。 (10分)
。 (10分)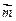 ,
, >=cos
>=cos
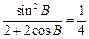 , (2分)
, (2分)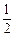 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B= (4分)
(4分) ,則
,則 =a+c+
=a+c+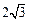
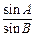 ,c=b·
,c=b·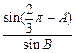 (2分)
(2分) =
=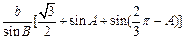 =
=
 (8分)
(8分)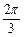 ),∴A-
),∴A-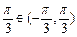 ,
, 時,
時,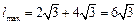 。 (10分)
。 (10分)

 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源:不詳 題型:單選題
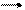 AB=a,
AB=a,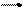 BC=b,
BC=b, CA=c,若a·(a+b
CA=c,若a·(a+b )<0,則△ABC是( )
)<0,則△ABC是( )A.直 角三角形 角三角形 | B.銳角三角形 | C.鈍角三角形 | D.無法判斷其形狀 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com