Question

已知方向向量為v＝(1，)的直線l過點(0，)和橢圓C：＝1(a＞b＞0)的焦點，且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上．

(1)求橢圓C的方程；

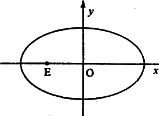
(2)是否存在過點E(－2，0)的直線m交橢圓C于點M、N，且滿足·＝cot∠MON≠0(SO為原點)？若存在，求直線m的方程；若不存在，請說明理由．

Answer 1

答案：
解析：

解：(1)直線l：y＝，① 　　過原點垂直于l的直線方程為y＝x，② 　　解①②得x＝． 　　因為橢圓中心O(0，0)關于直線l的對稱點在橢圓C的右準線上，所以＝3，又直線l過橢圓焦點，于是該焦點坐標為(2，0)． 　　∴c＝2，a2＝6，b2＝2． 　　故橢圓C的方程為＝1．③ 　　(2)設M(x1，y1)，N(x2，y2)， 　　當直線m不垂直于x軸時，直線my＝k(x＋2)， 　　代入③，整理得(3k2＋1)x2＋12k2x＋12k2－6＝0， 　　則x1＋x2＝，x1x2＝． 　　|MN|＝ 　　＝． 　　點O到直線MN的距離d＝． 　　∵·＝cot∠MON， 　　即||||cos∠MON＝≠0， 　　∴||||sin∠MON＝， 　　即(3k2＋1)． 　　整理得k2＝．∴k＝±． 　　當直線m垂直于x軸時，也滿足S△OMN＝． 　　故直線m的方程為y＝或y＝或x＝－2． 　　經檢驗上述直線均滿足·≠0， 　　所以所求直線方程為y＝或y＝或x＝－2．

提示：

本題主要考查直線、橢圓及平面向量的基本知識，平面解析幾何的基本方法和綜合解題的能力．利用橢圓的基本概念求得其標準方程，借助弦長公式，求出|MN|用k表示，求出S△DMN，利用其結果可知k的值．在解題中，要注意對斜率的討論．