
設函數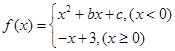 ,若
,若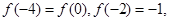
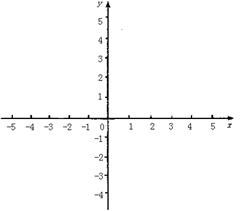
(1)求函數 的解析式;
的解析式;
(2)畫出函數 的圖象,并說出函數
的圖象,并說出函數 的單調區間;
的單調區間;
(3)若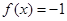 ,求相應
,求相應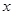 的值.
的值.
(1)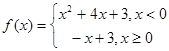 ;(2)增區間為
;(2)增區間為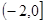 ,減區間為
,減區間為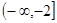 、
、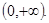 ;
;
(3)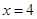 或x=-2。
或x=-2。
解析試題分析:解本小題關鍵是根據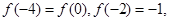 建立b,c的方程,從而解出b,c的值,確定f(x)的解析式,對于分段函數要注意分段求其單調區間.分段畫出其圖像.
建立b,c的方程,從而解出b,c的值,確定f(x)的解析式,對于分段函數要注意分段求其單調區間.分段畫出其圖像.
(1)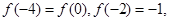
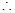
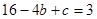 ,
,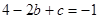 解得
解得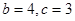
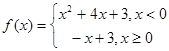 ------------------------------4
------------------------------4
(2)圖象略,--------------------------------------------------6
由圖象可知單調區間為: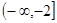 ,
,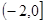 ,
,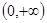 ,其中增區間為
,其中增區間為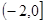 ,
,
減區間為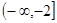 、
、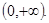 --------------------------------------8
--------------------------------------8
(3)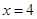 或x=-2----------------------------------------------------------------------12考點:本小題考查了函數的圖像及單調性以及解方程等知識.
或x=-2----------------------------------------------------------------------12考點:本小題考查了函數的圖像及單調性以及解方程等知識.
點評:分段函數在求解單調區間及最值時,要注意分段求解.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知函數f(x)=x2+(2+lga)x+lgb,f(-1)=-2.
(1)求a與b的關系式;
(2)若f(x)≥2x恒成立,求a、b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)某公司是專門生產健身產品的企業,第一批產品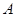 上市銷售40天內全部售完,該公司對第一批產品
上市銷售40天內全部售完,該公司對第一批產品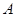 上市后的市場銷售進行調研,結果如圖(1)、(2)所示.其中(1)的拋物線表示的是市場的日銷售量與上市時間的關系;(2)的折線表示的是每件產品
上市后的市場銷售進行調研,結果如圖(1)、(2)所示.其中(1)的拋物線表示的是市場的日銷售量與上市時間的關系;(2)的折線表示的是每件產品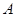 的銷售利潤與上市時間的關系.
的銷售利潤與上市時間的關系.
(1)寫出市場的日銷售量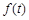 與第一批產品A上市時間t的關系式;
與第一批產品A上市時間t的關系式;
(2)第一批產品A上市后的第幾天,這家公司日銷售利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(文科題)(本小題12分)
要建造一個無蓋長方體水池,底面一邊長固定為8m,最大裝水量為72m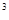 ,池底和池壁的造價分別為2
,池底和池壁的造價分別為2 元/
元/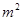 、
、 元/
元/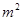 ,怎樣設計水池底的另一邊長和水池的高,才能使水池的總造價最低?最低造價是多少?
,怎樣設計水池底的另一邊長和水池的高,才能使水池的總造價最低?最低造價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上,在小艇出發時,輪船位于港口的O北偏西30°且與該港口相距20海里的A處,并正以30海里/小時的航行速度沿正東方向勻速行駛. 假設該小艇沿直線方向以v海里/小時的航行速度勻速行駛,經過t小時與輪船相遇.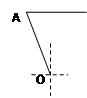
(Ⅰ)若希望相遇時小艇的航行距離最小,則小艇航行時間應為多少小時?
(Ⅱ)為保證小艇在30分鐘內(含30分鐘)能與輪船相遇,試確定小艇航行速度的最小值;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)某公司生產的新產品的成本是2元/件,售價是3元/件,
年銷售量為10萬件,為了獲得更好的效益,公司準備拿出一定的資金做廣告,根據經驗,每年投入的廣告費是 (萬元)時,產品的銷售量將是原銷售量的
(萬元)時,產品的銷售量將是原銷售量的 倍,且
倍,且 是
是 的二次函數,它們的關系如下表:
的二次函數,它們的關系如下表:
 | ··· | 1 | 2 | ··· | 5 | ··· |
 | ··· | 1.5 | 1.8 | ··· | 1.5 | ··· |
 與
與 的函數關系式;
的函數關系式; 成本費
成本費 廣告費,試寫出年利潤S(萬元)與廣告費
廣告費,試寫出年利潤S(萬元)與廣告費 (萬元)的函數關系式;并求出當廣告費
(萬元)的函數關系式;并求出當廣告費 為多少萬元時,年利潤S最大.
為多少萬元時,年利潤S最大.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com