分析:(1)先設拋物線C
1的方程再把點
M(,)代入方程即可求出拋物線C
1的方程及其焦點F的坐標;
(2)解一:先利用拋物線的準線經過雙曲線一個焦點F
1求出對應焦點坐標和c,再利用點
M(,)是雙曲線上的點,代入雙曲線定義2a=|MF
1-MF
2|中求出a就可求出雙曲線C
2的方程.
解二:先利用拋物線的準線經過雙曲線一個焦點F
1求出對應焦點坐標和c,再利用點
M(,)是雙曲線上的點適合雙曲線方程以及a
2+b
2=c
2,求出a
2和b
2就可求出雙曲線C
2的方程.
解答:解:解一:(1)由題意可設拋物線C
1的方程為y
2=2px.(2分)
把
M(,)代入方程為y
2=2px,得p=2(4分)
因此,拋物線C
1的方程為y
2=4x.(5分)
于是焦點F(1,0)(6分)
(2)拋物線C
1的準線方程為y=-1,
所以,F
1(-1,0)(7分)
而雙曲線C
2的另一個焦點為F(1,0),于是
2a=|MF1-MF|=|-|=1因此,
a=(9分)
又因為c=1,所以
b2=c2-a2=.
于是,雙曲線C
2的方程為
-=1.(12分)
解二:(1)同上(6分)
(2)拋物線C
1的準線方程為y=-1,
所以,F
1(-1,0)
而雙曲線C
2的另一個焦點為F(1,0),
∵點
M(,)在雙曲線上,∴
∴
-=1∴4a
4-37a
2+9=0
∴a
2=9(舍去)或
a2=,從而
b2=∴雙曲線方程為
-=1(12分)
點評:本題是對拋物線和雙曲線的綜合問題的考查.在求拋物線和雙曲線的標準方程時,一定要看清條件,分析出焦點所在位置在設方程.



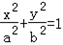 (a>b>0)的一個焦點
(a>b>0)的一個焦點 ,
,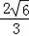 ).求拋物線C1及橢圓C2的方程.
).求拋物線C1及橢圓C2的方程.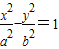 的一個焦點F1且垂直于C2的兩個焦點所在的軸,若拋物線C1與雙曲線C2的一個交點是
的一個焦點F1且垂直于C2的兩個焦點所在的軸,若拋物線C1與雙曲線C2的一個交點是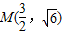 .
.