
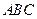 的邊長為4,
的邊長為4,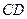 是
是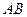 邊上的高,
邊上的高,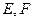 分別是
分別是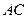 和
和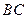 邊的中點,現將△
邊的中點,現將△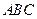 沿
沿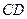 翻折成直二面角
翻折成直二面角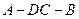 .
.
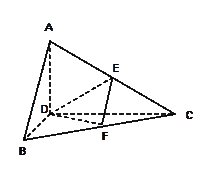
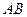 與平面
與平面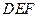 的位置關系,并說明理由;
的位置關系,并說明理由;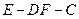 的余弦值;
的余弦值;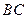 上是否存在一點
上是否存在一點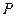 ,使
,使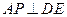 ?證明你的結論.
?證明你的結論.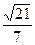

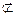 平面DEF,EF
平面DEF,EF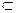 平面DEF.
平面DEF. 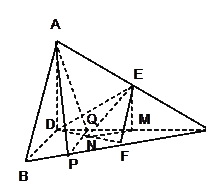
 EM∥AD ∴EM⊥平面BCD
EM∥AD ∴EM⊥平面BCD 1,MN=
1,MN=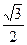
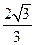 ,cos∠MNE=
,cos∠MNE=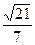 ………………………8分
………………………8分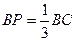 ,過P作PQ⊥CD與點Q,
,過P作PQ⊥CD與點Q,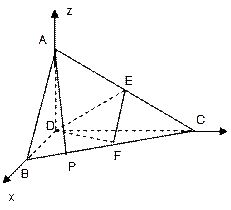
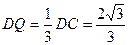 在等邊△ADE中,∠DAQ=30°
在等邊△ADE中,∠DAQ=30° 線DB、DC為x軸、y軸,建立空間直角坐標系,
線DB、DC為x軸、y軸,建立空間直角坐標系,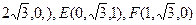 ……4分
……4分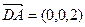 設平面EDF的法向量為
設平面EDF的法向量為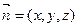
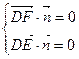 即
即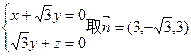
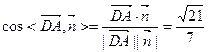 所以二面角E—DF—C的余弦值為
所以二面角E—DF—C的余弦值為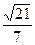 …8分
…8分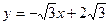
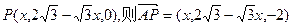
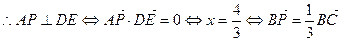 …………12分
…………12分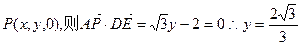
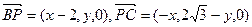 …………………12分
…………………12分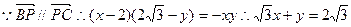
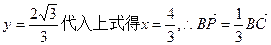
 …………….13分
…………….13分 

 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源:不詳 題型:解答題
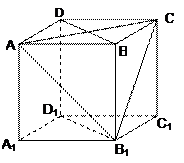
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 中,四邊形ABCD是邊長為2的正方形,四邊形
中,四邊形ABCD是邊長為2的正方形,四邊形 是邊長為1的正方形,
是邊長為1的正方形,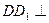 平面
平面 ,
,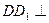 平面ABCD,DD1=2。
平面ABCD,DD1=2。
 與AC共面,
與AC共面, 與BD共面.
與BD共面. 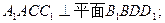
 的大小.
的大小.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

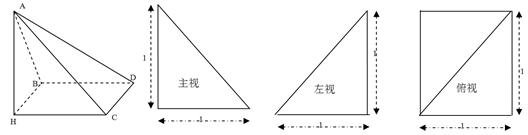
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
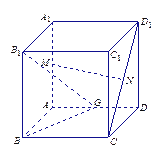
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
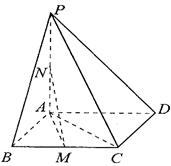
 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com