
 具有以下性質:①
具有以下性質:① ②若
②若 ,則
,則 ,且
,且 時,
時, .則稱集合
.則稱集合 是“好集”.
是“好集”. ,有理數(shù)集Q是否是“好集”,并說明理由;
,有理數(shù)集Q是否是“好集”,并說明理由; 是“好集”,求證:若
是“好集”,求證:若 ,則
,則 ;
; :若
:若 ,則必有
,則必有 ;
; :若
:若 ,且
,且 ,則必有
,則必有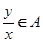 ;
; 是“好集”. (Ⅱ)
是“好集”. (Ⅱ)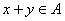 .
.  均為真命題..
均為真命題..  是“好集”.因為
是“好集”.因為 ,
, ,所以
,所以
 矛盾.這樣就確定集合
矛盾.這樣就確定集合 不是“好集”.有理數(shù)Q也采用同樣的方法,進行推證.
不是“好集”.有理數(shù)Q也采用同樣的方法,進行推證. 是“好集”,則
是“好集”,則 ,然后再根據(jù)x,y的任意性,可證明
,然后再根據(jù)x,y的任意性,可證明 .
. 不是“好集”. 理由是:假設集合
不是“好集”. 理由是:假設集合 是“好集”.
是“好集”.  ,
, ,所以
,所以 . 這與
. 這與 矛盾.…………2分
矛盾.…………2分 是“好集”. 因為
是“好集”. 因為 ,
, ,對任意的
,對任意的 ,有
,有 ,且
,且 時,
時, .所以有理數(shù)集
.所以有理數(shù)集 是“好集”. ………………………………4分
是“好集”. ………………………………4分 是“好集”,所以
是“好集”,所以  .若
.若 ,則
,則 ,即
,即 .
. ,即
,即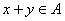 . …………………………6分
. …………………………6分 均為真命題. 理由如下: ………………………………………7分
均為真命題. 理由如下: ………………………………………7分 ,任取
,任取 , 若
, 若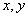 中有0或1時,顯然
中有0或1時,顯然 .
.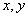 均不為0,1. 由定義可知:
均不為0,1. 由定義可知: .所以
.所以 ,即
,即 .
.  . 由(Ⅱ)可得:
. 由(Ⅱ)可得: ,即
,即 . 同理可得
. 同理可得 .
. 或
或 ,則顯然
,則顯然 .若
.若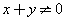 且
且 ,則
,則 .
. . 所以
. 所以  .由(Ⅱ)可得:
.由(Ⅱ)可得: .
. .綜上可知,
.綜上可知, ,即命題
,即命題 為真命題.若
為真命題.若 ,且
,且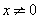 ,則
,則 .
. ,即命題
,即命題 為真命題. ……………………………………13分
為真命題. ……………………………………13分 

 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數(shù)學 來源:不詳 題型:填空題
 關于運算
關于運算 滿足:
滿足: ,都有
,都有 ;
; ,使得對一切
,使得對一切 ,都有
,都有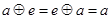 ,則稱
,則稱 關于運算
關于運算 為“融洽集”;現(xiàn)給出下列集合和運算:
為“融洽集”;現(xiàn)給出下列集合和運算:
 ① ②
① ②
 ④
④  ⑤
⑤ 關于運算
關于運算 為“融洽集”____________。(寫出所有“融洽集”的序號)
為“融洽集”____________。(寫出所有“融洽集”的序號)查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com