(滿分12分)已知點
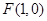
,直線
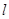
:
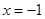
交
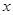
軸于點
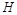
,點
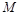
是
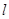
上的動點,過點
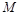
垂直于
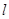
的直線與線段
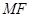
的垂直平分線交于點
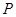
.
(Ⅰ)求點
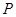
的軌跡
的方程;(Ⅱ)若 A、B為軌跡
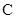
上的兩個動點,且
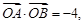
證明直線AB必過一定點,并求出該定點.
(1)
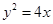
;(2)見解析。
試題分析:(1) 根據(jù)線段垂直平分線的定義所以點P到F的距離等于到直線
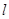
的距離.
所以,點P的軌跡是以F為焦點,
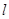
為準線的拋物線,且
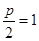
,
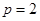
,
所以所求的軌跡方程為
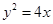
---------3分
(2) 設
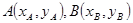
,直線AB的方程為
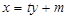
…………….5分
代入到拋物線方程整理得 則
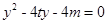
根據(jù)韋達定理
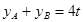
,即
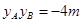
, …………8分
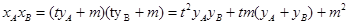
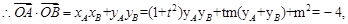
即
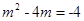
,解得m=2, …………11分
顯然,不論
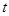
為何值,直線AB恒過定點
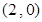
. ………………12分
點評:求軌跡方程的方法較多,首先應考慮定義法,即利用常見曲線的定義,從條件出發(fā)確定幾何元素。直線與圓錐曲線的位置關系問題,韋達定理常常用到。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
已知橢圓
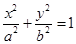
(
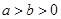
)中,
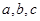
成等比數(shù)列,則橢圓的離心率為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知拋物線
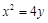
的焦點
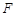
和點
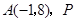
為拋物線上一點,則
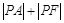
的最小值是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
(1)焦點在x軸上的橢圓的一個頂點為A(2,0),其長軸長是短軸長的2倍,求橢圓的標準方程.
(2)已知雙曲線的一條漸近線方程是
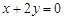
,并經(jīng)過點
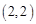
,求此雙曲線的標準方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知橢圓
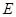
的焦點在
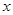
軸上,離心率為
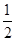
,對稱軸為坐標軸,且經(jīng)過點
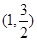
.
(I)求橢圓
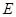
的方程;
(II)直線
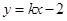
與橢圓
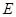
相交于
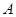
、
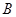
兩點,
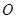
為原點,在
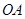
、
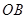
上分別存在異于
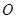
點的點
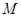
、
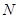
,使得
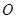
在以
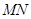
為直徑的圓外,求直線斜率
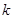
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
雙曲線
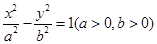
,過其一個焦點且垂直于實軸的直線與雙曲線交于
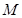
、
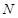
兩點,O是坐標原點,滿足
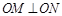
,則雙曲線的離心率為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
以
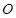
為中心,
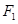
,
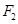
為兩個焦點的橢圓上存在一點
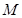
,滿足
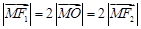
,則該橢圓的離心率為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)
已知橢圓
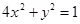
及直線
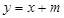
.
(1)當
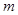
為何值時,直線與橢圓有公共點?
(2)若直線被橢圓截得的弦長為
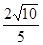
,求直線的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線C:
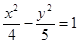
的右焦點為
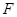
,過
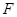
的直線
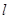
與C交于兩點
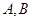
,若
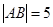
,則滿足條件的
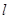
的條數(shù)為
.
查看答案和解析>>

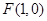 ,直線
,直線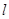 :
: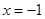 交
交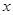 軸于點
軸于點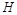 ,點
,點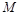 是
是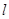 上的動點,過點
上的動點,過點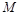 垂直于
垂直于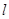 的直線與線段
的直線與線段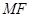 的垂直平分線交于點
的垂直平分線交于點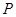 .
.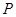 的軌跡
的軌跡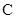 的方程;(Ⅱ)若 A、B為軌跡
的方程;(Ⅱ)若 A、B為軌跡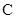 上的兩個動點,且
上的兩個動點,且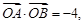 證明直線AB必過一定點,并求出該定點.
證明直線AB必過一定點,并求出該定點. 名校課堂系列答案
名校課堂系列答案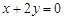 ,并經(jīng)過點
,并經(jīng)過點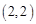 ,求此雙曲線的標準方程.
,求此雙曲線的標準方程.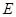 的焦點在
的焦點在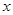 軸上,離心率為
軸上,離心率為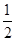 ,對稱軸為坐標軸,且經(jīng)過點
,對稱軸為坐標軸,且經(jīng)過點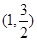 .
.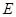 的方程;
的方程;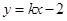 與橢圓
與橢圓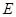 相交于
相交于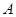 、
、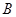 兩點,
兩點, 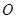 為原點,在
為原點,在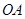 、
、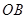 上分別存在異于
上分別存在異于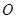 點的點
點的點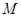 、
、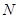 ,使得
,使得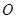 在以
在以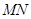 為直徑的圓外,求直線斜率
為直徑的圓外,求直線斜率 的取值范圍.
的取值范圍.