已知函數f(x)=exlnx.
(1)求函數f(x)的單調區間;
(2)設x>0,求證:f(x+1)>e2x-1;
(3)設n∈N*,求證:ln(1×2+1)+ln(2×3+1)+…+ln[n(n+1)+1]>2n-3.
【答案】
分析:由題意(1)有函數解析式可以先求出函數的定義域,再對函數求導,令導函數大于0解出函數的單調遞增區間,令導函數小于0解出函數的減區間;
(2)利用分析法分析出要證明的等價的不等式令
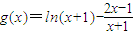
,由
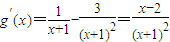
,得出函數等價求解函數在定義域上的最小值即可求得;
(3)有(2)得
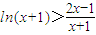
,即
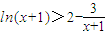
,然后把x被k(k+1)代替,即可.
解答:解:(1)定義域為(0,+∞),由f′(x)=e
xlnx(lnx+1),
令
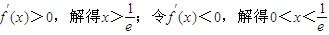
.
故f(x)的增區間:
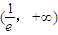
,減區間:

,
(2)即證:
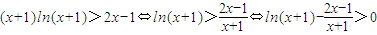
令
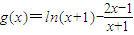
,由
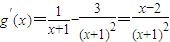
,
令g′(x)=0,得x=2,且g(x)在(0,2)↓,在(2,+∞)↑,所以g(x)
min=g(2)=ln3-1,
故當x>0時,有g(x)≥g(2)=ln3-1>0得證,
(3)由(2)得
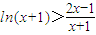
,即
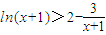
,
所以
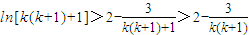
,
則:ln(1×2+1)+ln(2×3+1)+…+ln[(n(n+1)]+1
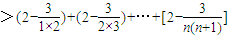
=
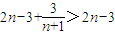
.
點評:此題考查了利用導數求函數的單調區間,還考查了分析法證明不不等式,還考查了不等式證明中的簡單放縮及求和時的裂項相消法.

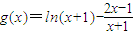 ,由
,由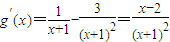 ,得出函數等價求解函數在定義域上的最小值即可求得;
,得出函數等價求解函數在定義域上的最小值即可求得;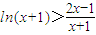 ,即
,即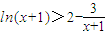 ,然后把x被k(k+1)代替,即可.
,然后把x被k(k+1)代替,即可.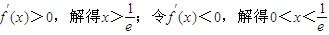 .
.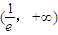 ,減區間:
,減區間: ,
,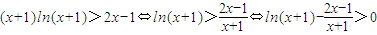
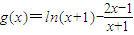 ,由
,由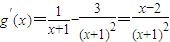 ,
,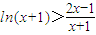 ,即
,即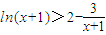 ,
,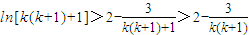 ,
,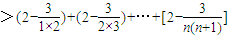 =
=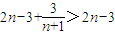 .
.
