
在正方體ABCD—A1B1C1D1中,若E是A1C1的中點,則直線CE垂直于( ) 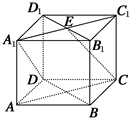
| A.AC | B.BD | C.A1D | D.A1D |
B
解析試題分析:以A為原點,AB、AD、AA1所在直線分別為x,y,z軸建空間直角坐標系,設正方體棱長為1,則A(0,0,0),C(1,1,0),B(1,0,0),D(0,1,0),A1(0,0,1),E(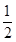 ,
,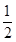 ,1),所以
,1),所以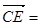 (
(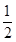 ,
,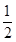 ,1),
,1),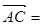 (1,1,0),
(1,1,0),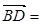 (-1,1,0),
(-1,1,0),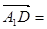 (0,1,-1),
(0,1,-1),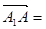 (0,0,-1),顯然
(0,0,-1),顯然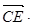
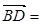 0,即CE⊥BD. 故選 B.
0,即CE⊥BD. 故選 B.
考點:線面垂直的判定定理。
點評:本題所用的方法為:利用空間直角坐標系表示出向量的坐標,再利用兩個向量的數量積等于0,證明兩個向量垂直。本題也可以用綜合法:在正方體ABCD—A1B1C1D1中,易知BD⊥面ACC1A1,又因為CE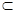 面ACC1A1,所以BD⊥CE。
面ACC1A1,所以BD⊥CE。


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:單選題
設 、b是兩條不同的直線,
、b是兩條不同的直線, 、
、 是兩個不同的平面,則下列四個命題中正確的是( )
是兩個不同的平面,則下列四個命題中正確的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,則b∥ ,則b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,則 ,則 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,則 ,則  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,則 ,則 ⊥ ⊥ |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
設l,m,n為三條不同的直線,α、β為兩個不同的平面,下列命題中正確的個數是( )
① 若l⊥α,m∥β,α⊥β則l⊥m ② 若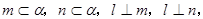 則l⊥α
則l⊥α
③ 若l∥m,m∥n,l⊥α,則n⊥α ④ 若l∥m,m⊥α,n⊥β,α∥β,則l∥n
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
如圖,已知正方體ABCD-A1B1C1D1,E、F分別是平面A1B1C1D1和ADD1A1的中心,則EF和CD所成的角是( ).
| A.60° | B.45° | C.30° | D.90° |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
直線a、b、c及平面α、β,下列命題正確的是( )
A.若a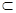 α,b α,b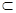 α,c⊥a, c⊥b 則c⊥α α,c⊥a, c⊥b 則c⊥α | B.若b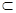 α, a//b則 a//α α, a//b則 a//α |
| C.若a//α,α∩β=b則a//b | D.若a⊥α, b⊥α 則a//b |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知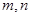 是兩條不重合的直線,
是兩條不重合的直線,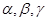 是三個兩兩不重合的平面, 給出下列四個命題:
是三個兩兩不重合的平面, 給出下列四個命題:
①若 ; ②若
; ②若 ;
;
③若 ;
;
④若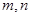 是異面直線,
是異面直線,
其中真命題是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com