Question

直線y=a與函數f(x)=x³-3x的圖象有相異的三個交點，求a的取值范圍.

Answer 1

分析：∵y=a與f(x)=x³-3x的圖象有相異的三個交點,知f(x)=x³-3x有兩個“拐點”(已具備),且兩“拐點”分布在y=a的兩側,即有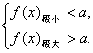故需求f(x)的極值.

解：研究函數y=a與函數f(x)=x³-3x的交點個數，由于y=a是一條平行于x軸(a=0時與x軸重合)的直線，

∴只需研究函數f(x)=x³-3x圖象的變化趨勢即可.

∵f′(x)=3x²-3=3(x-1)(x+1),∴在區間(-∞,-1]上,f(x)遞增；

    在［-1,1］上,f(x)遞減；

    在［1,+∞)上,f(x)遞增.

∴［f(x)］_極小值=-2，［f(x)］_極大值=2.

    因此，要使y=a與函數f(x)的圖象有相異的三個交點，必須有a∈(-2,2).