中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

過圓錐曲線焦點(diǎn)的直線與此圓錐曲線交于P1、P2兩點(diǎn)，以P1P2為直徑的圓與此焦點(diǎn)對應(yīng)的準(zhǔn)線相切，則此圓錐曲線是（    ）

A.橢圓             B.雙曲線             C.拋物線            D.不確定

C


解析:

如圖所示，設(shè)過拋物線y2=2px（p>0）焦點(diǎn)F的弦為AB，弦中點(diǎn)為M，A、B、M在準(zhǔn)線x=-上的垂足為A′、B′、M′，則MM′為梯形AA′B′B的中位線.

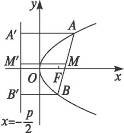
所以有|MM′|=（|AA′|+|BB′|）.

由拋物線定義|AA′|+|BB′|=|AF|+|BF|=|AB|，

∴|MM′|=|AB|.

∴以過焦點(diǎn)F的直線與拋物線的交點(diǎn)所成線段AB為直徑的圓與準(zhǔn)線相切.

故選C.

同理可得當(dāng)相離時，是雙曲線；當(dāng)相交時，是橢圓.以上可作為結(jié)論記住，提高解題速度.

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：

（理）過圓錐曲線焦點(diǎn)F的直線被曲線截得的弦稱為焦點(diǎn)弦，若拋物線y2=2px（p＞0）的焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則有結(jié)論
1
m
+
1
n
=
2
p
．借助獲得這一結(jié)論的思想方法可以得到：若橢圓
x2
a2
+
y2
b2
=1 (a＞b＞0)的一個焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則
1
m
+
1
n
=
2a
b2
2a
b2
．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

（理）過圓錐曲線焦點(diǎn)F的直線被曲線截得的弦稱為焦點(diǎn)弦，若拋物線y2=2px（p＞0）的焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則有結(jié)論
1
m
+
1
n
=
2
p
．借助獲得這一結(jié)論的思想方法可以得到：若橢圓
x2
a2
+
y2
b2
=1 (a＞b＞0)的一個焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則
1
m
+
1
n
=______．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

（理）過圓錐曲線焦點(diǎn)F的直線被曲線截得的弦稱為焦點(diǎn)弦，若拋物線y2=2px（p＞0）的焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則有結(jié)論
1
m
+
1
n
=
2
p
．借助獲得這一結(jié)論的思想方法可以得到：若橢圓
x2
a2
+
y2
b2
=1 (a＞b＞0)的一個焦點(diǎn)將焦點(diǎn)弦分成長為m，n的兩段，則
1
m
+
1
n
=______．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：

過圓錐曲線焦點(diǎn)的直線與此圓錐曲線交于P1、P2兩點(diǎn)，以P1P2為直徑的圓與此焦點(diǎn)對應(yīng)的準(zhǔn)線相切，則此圓錐曲線是（    ）

A.橢圓             B.雙曲線             C.拋物線            D.不確定

查看答案和解析>>