(1) ,
,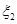 的分布列為:
的分布列為:

| 1.25
| 1.125
| 1
| 0.9
| 0.8
|
P
| 0.15
| 0.15
| 0.35
| 0.15
| 0.2
|
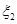
| 1.44
| 1.2
| 1
| 0.96
| 0.8
|
P
| 0.08
| 0.24
| 0.18
| 0.2
| 0.3
|
(2)實施方案二的概率更大
(3)第一個方案的平均利潤更大
解析試題分析:(1) 根據題意,由于實施方案一,預計第一年可以使出口額恢復到危機前的 倍、
倍、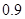 倍、
倍、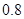 倍的概率分別為
倍的概率分別為 、
、 、
、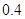 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的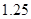 倍、
倍、 倍的概率分別為
倍的概率分別為 、
、 。若實施方案二,預計第一年可以使出口額恢復到危機前的
。若實施方案二,預計第一年可以使出口額恢復到危機前的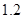 倍、
倍、 倍、
倍、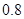 倍的概率分別為
倍的概率分別為 、
、 、
、 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的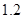 倍、
倍、 倍的概率分別為
倍的概率分別為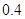 、
、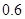 ,那么可知
,那么可知 ,
,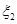 的分布列為:
的分布列為:

| 1.25
| 1.125
| 1
| 0.9
| 0.8
|
P
| 0.15
| 0.15
| 0.35
| 0.15
| 0.2
|
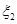
| 1.44
| 1.2
| 1
| 0.96
| 0.8
|
P
| 0.08
| 0.24
|
練習冊系列答案
相關習題
科目:高中數學
來源:
題型:解答題
某小組共有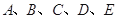 五位同學,他們的身高(單位:米)以及體重指標(單位:千克/米2)如下表所示: 五位同學,他們的身高(單位:米)以及體重指標(單位:千克/米2)如下表所示:
| A
| B
| C
| D
| E
| 身高
| 1.69
| 1.73
| 1.75
| 1.79
| 1.82
| 體重指標
| 19.2
| 25.1
| 18.5
| 23.3
| 20.9
|
(1)從該小組身高低于1.80的同學中任選2人,求選到的2人身高都在1.78以下的概率; (2)從該小組同學中任選2人,求選到的2人的身高都在1.70以上且體重指標都在[18.5,23.9)中的概率.
查看答案和解析>>
科目:高中數學
來源:
題型:解答題
通過隨機詢問某校110名高中學生在購買食物時是否看營養說明,得到如下的列聯表:
性別與看營養說明列聯表 單位: 名
| 男
| 女
| 總計
| 看營養說明
| 50
| 30
| 80
| 不看營養說明
| 10
| 20
| 30
| 總計
| 60
| 50
| 110
|
(1)從這50名女生中按是否看營養說明采取分層抽樣,抽取一個容量為10的樣本,問樣本中看與不看營養說明的女生各有多少名? (2)根據以上列聯表,能否在犯錯誤的概率不超過0.01的前提下認為性別與是否看營養說明之間有關系? 下面的臨界值表供參考: 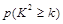
| 0.15
| 0.10
| 0.05
| 0.025
| 0.010
| 0.005
| 0.001
| 
| 2.072
| 2.706
| 3.841
| 5.024
| 6.635
| 7.879
| 10.828
|
(參考公式:  ,其中  ) 
查看答案和解析>>
科目:高中數學
來源:
題型:解答題
某商場經銷某商品,根據以往資料統計,顧客采用的付款期數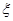 的分布列為 的分布列為
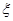
| 1
| 2
| 3
| 4
| 5
| 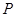
| 0.4
| 0.2
| 0.2
| 0.1
| 0.1
|
商場經銷一件該商品,采用1期付款,其利潤為200元;分2期或3期付款,其利潤為250元;分4期或5期付款,其利潤為300元.  表示經銷一件該商品的利潤. (Ⅰ)求事件 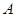 :“購買該商品的3位顧客中,至少有1位采用1期付款”的概率 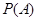 ; (Ⅱ)求  的分布列及期望 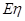 與方差D 
查看答案和解析>>
科目:高中數學
來源:
題型:解答題
某市2010年4月1日—4月30日對空氣污染指數的監測數據如下(主要污染物為可吸入顆粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成頻率分布表;
(2)作出頻率分布直方圖;
(3)根據國家標準,污染指數在0~50之間時,空氣質量為優;在51~100之間時,為良;在101~150之間時,為輕微污染;在151~200之間時,為輕度污染.
請你依據所給數據和上述標準,對該市的空氣質量給出一個簡短評價.
查看答案和解析>>
科目:高中數學
來源:
題型:解答題
兩枚質量均勻的正方體骰子,六個面上分別標有數字1、2、3、4、5、6,拋擲兩枚骰子.記兩枚骰子朝上的面上的數字分別為p,q,若把p,q分別作為點A的橫坐標和縱坐標,
(1)用列表法或樹狀圖表示出點A(p,q)所有可能出現的結果;
(2)求點A(p,q)在函數y=x-1的圖象上的概率.
查看答案和解析>>
|

 倍、
倍、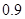 倍、
倍、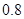 倍的概率分別為
倍的概率分別為 、
、 、
、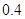 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的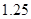 倍、
倍、 倍的概率分別為
倍的概率分別為 、
、 。若實施方案二,預計第一年可以使出口額恢復到危機前的
。若實施方案二,預計第一年可以使出口額恢復到危機前的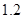 倍、
倍、 倍、
倍、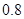 倍的概率分別為
倍的概率分別為 、
、 、
、 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的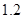 倍、
倍、 倍的概率分別為
倍的概率分別為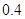 、
、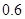 。實施每種方案第一年與第二年相互獨立。令
。實施每種方案第一年與第二年相互獨立。令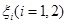 表示方案
表示方案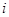 實施兩年后出口額達到危機前的倍數。
實施兩年后出口額達到危機前的倍數。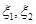 的分布列;
的分布列; 萬元、
萬元、 萬元、
萬元、 萬元,問實施哪種方案的平均利潤更大?
萬元,問實施哪種方案的平均利潤更大? ,
,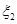 的分布列為:
的分布列為:
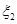
 倍、
倍、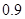 倍、
倍、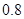 倍的概率分別為
倍的概率分別為 、
、 、
、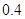 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的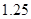 倍、
倍、 倍的概率分別為
倍的概率分別為 、
、 。若實施方案二,預計第一年可以使出口額恢復到危機前的
。若實施方案二,預計第一年可以使出口額恢復到危機前的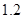 倍、
倍、 倍、
倍、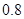 倍的概率分別為
倍的概率分別為 、
、 、
、 ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的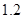 倍、
倍、 倍的概率分別為
倍的概率分別為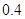 、
、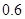 ,那么可知
,那么可知 ,
,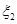 的分布列為:
的分布列為:


聊城中考系列答案
學業測評一卷通小學升學試題匯編系列答案
小學單元綜合練習與檢測系列答案
實驗探究報告練習冊系列答案
單元學習體驗與評價系列答案
黃岡小狀元小學升學考試沖刺復習卷系列答案
畢業總復習沖刺卷系列答案
學習指導系列答案
隨堂同步練習系列答案
數學奧賽天天練系列答案
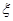 為取得紅球的個數.
為取得紅球的個數. 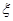 的分布列;
的分布列;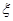 的數學期望
的數學期望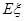 .
.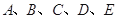 五位同學,他們的身高(單位:米)以及體重指標(單位:千克/米2)如下表所示:
五位同學,他們的身高(單位:米)以及體重指標(單位:千克/米2)如下表所示: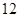 名工人,隨機抽取
名工人,隨機抽取 名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數. 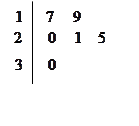
 名工人中有幾名優秀工人;
名工人中有幾名優秀工人; 名工人中,任取
名工人中,任取 人,求恰有
人,求恰有 名優秀工人的概率.
名優秀工人的概率. 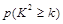

 ,其中
,其中 )
)
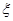 的分布列為
的分布列為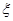
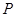
 表示經銷一件該商品的利潤.
表示經銷一件該商品的利潤.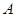 :“購買該商品的3位顧客中,至少有1位采用1期付款”的概率
:“購買該商品的3位顧客中,至少有1位采用1期付款”的概率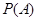 ;
; 的分布列及期望
的分布列及期望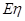 與方差D
與方差D
 小時收費
小時收費 元,超過
元,超過 小時的部分每小時收費
小時的部分每小時收費 元(不足
元(不足 小時的部分按
小時的部分按 小時計算).現有甲、乙二人在該商區臨時停車,兩人停車都不超過
小時計算).現有甲、乙二人在該商區臨時停車,兩人停車都不超過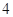 小時.
小時. 小時以上且不超過
小時以上且不超過 小時的概率為
小時的概率為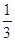 ,停車付費多于
,停車付費多于 元的概率為
元的概率為 ,求甲停車付費恰為
,求甲停車付費恰為 元的概率;
元的概率; 元的概率.
元的概率.