
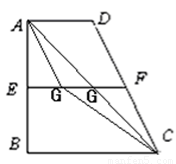
如圖,直角梯形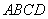 中,
中,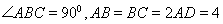 ,點(diǎn)
,點(diǎn)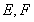 分別是
分別是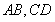 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)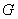 在
在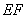 上,沿
上,沿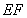 將梯形
將梯形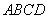 翻折,使平面
翻折,使平面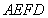
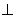 平面
平面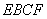 .
.
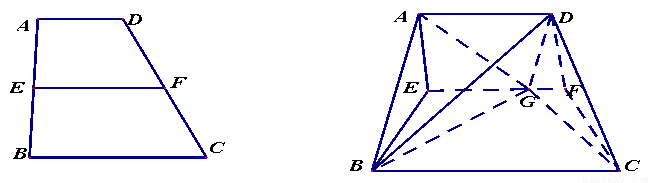
(1)當(dāng)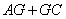 最小時(shí),求證:
最小時(shí),求證: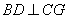 ;
;
(2)當(dāng)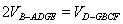 時(shí),求二面角
時(shí),求二面角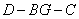 平面角的余弦值.
平面角的余弦值.
(1)參考解析;(2)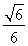
【解析】
試題分析:(1)因?yàn)楫?dāng)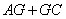 最小時(shí),及連結(jié)AC與EF的交點(diǎn)即為G點(diǎn),通過三角形的相似可得到EG的長(zhǎng)度.需要證明直線與直線垂直,根據(jù)題意建立空間直角坐標(biāo)系,即可得到相關(guān)各點(diǎn)的坐標(biāo),從而寫出相關(guān)向量,即可判斷直線的垂直關(guān)系.
最小時(shí),及連結(jié)AC與EF的交點(diǎn)即為G點(diǎn),通過三角形的相似可得到EG的長(zhǎng)度.需要證明直線與直線垂直,根據(jù)題意建立空間直角坐標(biāo)系,即可得到相關(guān)各點(diǎn)的坐標(biāo),從而寫出相關(guān)向量,即可判斷直線的垂直關(guān)系.
(2)由題意所給的體積關(guān)系可確定點(diǎn)G的位置,求二面角關(guān)鍵是轉(zhuǎn)化為兩平面的法向量的夾角,由于平面BCG的法向量易得,關(guān)鍵是求出平面DGB的法向量.通過待定系數(shù)法即可求得,還需判斷二面角與法向量夾角的大小關(guān)系.解法二用到的推理論證的數(shù)學(xué)思想很重要.
試題解析:(1)證明:∵點(diǎn)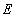 、
、 分別是
分別是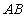 、
、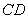 的中點(diǎn),∴EF//BC
的中點(diǎn),∴EF//BC
又∠ABC=90°∴AE⊥EF,∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE, 又BE⊥EF,
如圖建立空間坐標(biāo)系E﹣xyz.
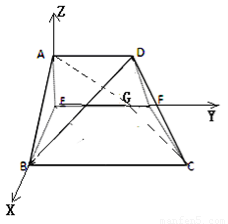
翻折前,連結(jié)AC交EF于點(diǎn)G,此時(shí)點(diǎn)G使得AG+GC最小.
EG= BC=2,又∵EA=EB=2.
BC=2,又∵EA=EB=2.
則A(0,0,2),B(2,0,0),C(2,4,0), D(0,2,2),E(0,0,0),G(0,2,0),
∴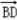 =(﹣2,2,2),
=(﹣2,2,2), =(-2,-2,0)
=(-2,-2,0)
∴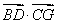 =(﹣2,2,2)(-2,-2,0)=0,
=(﹣2,2,2)(-2,-2,0)=0,
∴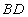 ⊥
⊥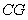
(2)解法一:設(shè)EG=k,
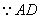 ∥平面
∥平面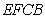 ,
, 點(diǎn)D到平面EFCB的距離為即為點(diǎn)A到平面EFCB的距離.
點(diǎn)D到平面EFCB的距離為即為點(diǎn)A到平面EFCB的距離.

 [(3- k)+4]×2=7-k
[(3- k)+4]×2=7-k
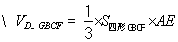 =
=
又 =
=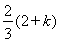 ,
,

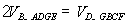 ,
,
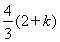 =
=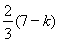 ,
,
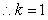 即EG=1
即EG=1
設(shè)平面DBG的法向量為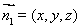 ,∵G(0,1,0),
,∵G(0,1,0),
∴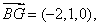
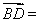 (-2,2,2),
(-2,2,2),
則  ,即
,即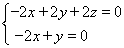
取x=1,則y=2,z=-1,∴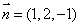
面BCG的一個(gè)法向量為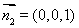
則cos<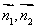 >=
>= 由于所求二面角D-BF-C的平面角為銳角,
由于所求二面角D-BF-C的平面角為銳角,
所以此二面角平面角的余弦值為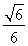
(2)解法二:由解法一得EG=1,過點(diǎn)D作DH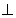 EF,垂足H,過點(diǎn)H作BG延長(zhǎng)線的垂線垂足O,連接OD.
EF,垂足H,過點(diǎn)H作BG延長(zhǎng)線的垂線垂足O,連接OD.
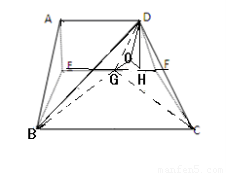
∵平面AEFD⊥平面EBCF, DH
DH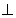 平面EBCF,
平面EBCF, OD
OD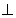 OB,所以
OB,所以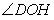 就是所求的二面角
就是所求的二面角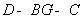 的平面角.由于HG=1,在
的平面角.由于HG=1,在 OHG中
OHG中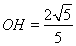 ,
,
又DH=2,在 DOH中
DOH中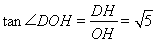
所以此二面角平面角的余弦值為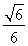
考點(diǎn):1.圖形的翻折問題.2.線面垂直的判定.3.二面角的求法.4.空間坐標(biāo)系中的運(yùn)算.5.空間想象能力.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
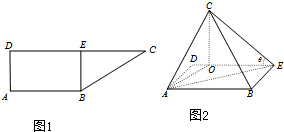 (2012•深圳一模)如圖,直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD=
(2012•深圳一模)如圖,直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆天津市高二第一次月考數(shù)學(xué)試卷(解析版) 題型:解答題
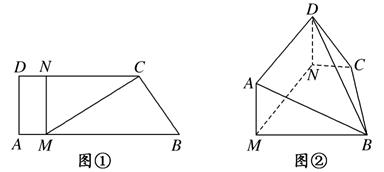
(14分)如圖①,直角梯形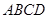 中,
中, ,點(diǎn)
,點(diǎn)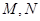 分別在
分別在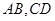 上,且
上,且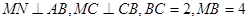 ,現(xiàn)將梯形
,現(xiàn)將梯形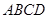 A沿
A沿 折起,使平面
折起,使平面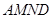 與平面
與平面 垂直(如圖②).
垂直(如圖②).
(1)求證: 平面
平面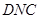 ;
;
(2)當(dāng) 時(shí),求二面角
時(shí),求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
如圖,直角梯形![]() 中,
中,![]() //
//![]() ,
,![]() ,
, ![]() ,
,![]() ,
,
![]() 丄底面
丄底面![]() ,
, ![]() 丄底面
丄底面![]() 且有
且有![]() .
.
(1)求證:![]() 丄
丄![]() ;
;
(2)若線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年浙東北三校高二下學(xué)期期中聯(lián)考數(shù)學(xué)(理) 題型:解答題
如圖,直角梯形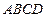 中,
中,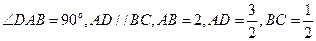
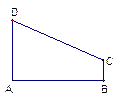
橢圓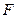 以
以 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn) ,
,
(1)建立適當(dāng)?shù)闹苯亲鴺?biāo)系,求橢圓的方程;
(2)若點(diǎn)E滿足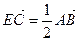 是否存在斜率
是否存在斜率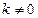 的直線
的直線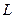 與橢圓
與橢圓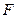 交于
交于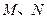 兩點(diǎn),且
兩點(diǎn),且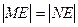 ,若存在,求
,若存在,求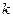 的取值范圍;若不存在,說明理由。
的取值范圍;若不存在,說明理由。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com