
 +3x-
+3x- .
. +3x-
+3x- .的函數圖象,可得到函數y=
.的函數圖象,可得到函數y=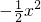 的圖象;
的圖象; ,故頂點橫坐標為3,代入解析式,即f(3)=2,故頂點坐標為(3,2).(2分)
,故頂點橫坐標為3,代入解析式,即f(3)=2,故頂點坐標為(3,2).(2分) +3x-
+3x- =0,解得x=1或x=-5,故與x軸交點坐標為(1,0)或(5,0)(4分)
=0,解得x=1或x=-5,故與x軸交點坐標為(1,0)或(5,0)(4分) .故與y軸交點坐標為(0,
.故與y軸交點坐標為(0, )(6分)
)(6分) ,
, ,即g(x)的解析式為
,即g(x)的解析式為 ,又
,又 .(16分)
.(16分) ,即g(x)的解析式為
,即g(x)的解析式為 ,又g(x)的頂點坐標為(2,2),可算出b,c值.
,又g(x)的頂點坐標為(2,2),可算出b,c值.

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| f(x) | x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com