
某公司欲招聘員工,從1000名報名者中篩選200名參加筆試,按筆試成績擇優取50名面試,再從面試對象中聘用20名員工.
(Ⅰ)求每個報名者能被聘用的概率;
(Ⅱ)隨機調查了24名筆試者的成績如下表所示:
| 分數段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人數 | 1 | 2 | 6 | 9 | 5 | 1 |
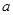 、
、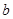 、
、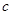 、
、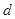 和二女
和二女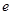 、
、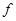 中選派兩人參加某項培訓,則選派結果為一男一女的概率是多少?
中選派兩人參加某項培訓,則選派結果為一男一女的概率是多少? (Ⅰ)每個報名者能被聘用的概率為0.02;(Ⅱ)預測面試的分數線大約為80分;(Ⅲ)選派結果為一男一女的概率為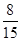 .
.
解析試題分析:(Ⅰ)求每個報名者能被聘用的概率,利用古典概型求概率是解決本題的關鍵,根據每個人入選的概率相等可以計算出所求的概率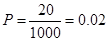 ;(Ⅱ)利用概率是樣本頻率的近似值,通過對應成比例,設24名筆試者中有
;(Ⅱ)利用概率是樣本頻率的近似值,通過對應成比例,設24名筆試者中有 名可以進入面試,依樣本估計總體可得:
名可以進入面試,依樣本估計總體可得: ,解得
,解得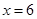 ,從樣本查處第六名的分數,就得出被聘用的最低分數線;(Ⅲ)求選派結果為一男一女的概率,利用古典概型求概率是解決本題的關鍵,可以列舉出樣本空間的所有情況,從聘用的四男、二女中選派兩人的基本事件有:(
,從樣本查處第六名的分數,就得出被聘用的最低分數線;(Ⅲ)求選派結果為一男一女的概率,利用古典概型求概率是解決本題的關鍵,可以列舉出樣本空間的所有情況,從聘用的四男、二女中選派兩人的基本事件有:(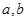 ), (
), (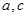 ),(
),(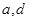 ),(
),(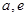 ),(
),(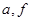 ),(
),(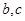 ),(
),(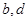 ),(
),(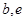 ),(
),(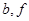 ), (
), (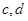 ),(
),(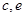 ),(
),(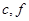 ),(
),(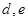 ),(
),(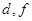 ),(
),(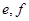 ),共15種,并求出所求事件的所有情況,即選派一男一女的基本事件有:(
),共15種,并求出所求事件的所有情況,即選派一男一女的基本事件有:( 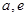 ) , (
) , ( 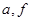 ) , (
) , ( 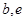 ) ,(
) ,( 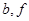 ) , (
) , (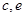 ),(
),( 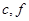 ) , (
) , ( 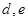 ) ,(
) ,( 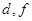 ),共8種,通過算起比值得到所求的概率.
),共8種,通過算起比值得到所求的概率.
試題解析:(Ⅰ)設每個報名者能被聘用的概率為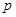 ,依題意有:
,依題意有: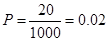 .
.
答:每個報名者能被聘用的概率為0.02. 3分
(Ⅱ)設24名筆試者中有 名可以進入面試,依樣本估計總體可得:
名可以進入面試,依樣本估計總體可得: ,解得:
,解得: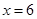 ,從表中可知面試的分數線大約為80分.
,從表中可知面試的分數線大約為80分.
答:可以預測面試的分數線大約為80分. 7分
(Ⅲ)從聘用的四男、二女中選派兩人的基本事件有:
(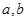 ),(
),(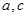 ),(
),(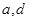 ),(
),(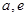 ),(
),(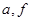 ),(
),(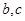 ),(
),(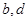 ),(
),(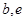 ),(
),(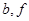 ), (
), (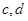 ),(
),(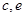 ),(
),(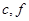 ),(
),(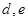 ),(
),(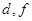 ),(
),(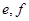 ),共15種. 10分
),共15種. 10分
選派一男一女參加某項培訓的種數有( 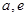 ) , (
) , ( 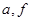 ) , (
) , ( 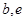 ) ,(
) ,( 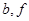 ) , (
) , (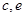 ),(
),( 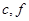 ) , (
) , ( 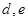 ) ,(
) ,( 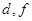 ),共8種, 12分
),共8種, 12分
所以選派結果為一男一女的概率為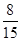 .
.
答:選派結果為一男一女的概率為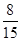 . 13分
. 13分
考點:等可能事件的概率.


科目:高中數學 來源: 題型:解答題
一汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表所示(單位輛),若按A,B,C三類用分層抽樣的方法在這個月生產的轎車中抽取50輛,則A類轎車有10輛
| | 轎車A | 轎車B | 轎車C |
| 舒適型 | 100 | 150 | z |
| 標準型 | 300 | 450 | 600 |
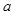 記這8輛轎車的得分的平均數為
記這8輛轎車的得分的平均數為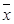 ,定義事件
,定義事件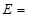 {
{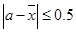 ,且函數
,且函數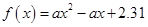 沒有零點},求事件
沒有零點},求事件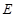 發生的概率
發生的概率 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現有10道題,其中6道甲類題,4道乙類題,張同學從中任取3道題解答.
(I)求張同學至少取到1道乙類題的概率;
(II)已知所取的3道題中有2道甲類題,1道乙類題.設張同學答對甲類題的概率都是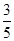 ,答對每道乙類題的概率都是
,答對每道乙類題的概率都是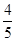 ,且各題答對與否相互獨立.用
,且各題答對與否相互獨立.用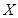 表示張同學答對題的個數,求
表示張同學答對題的個數,求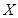 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設關于 的一元二次方程
的一元二次方程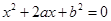 .
.
(1)若 是從
是從 、
、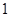 、
、 、
、 四個數中任取的一個數,
四個數中任取的一個數, 是從
是從 、
、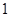 、
、 三個數中任取的一個數,求上述方程有實根的概率;
三個數中任取的一個數,求上述方程有實根的概率;
(2)若 是從區間
是從區間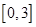 任取的一個數,
任取的一個數, 是從區間
是從區間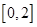 任取的一個數,求上述方程有實根的概率.
任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
高三某班有兩個數學課外興趣小組,第一組有 名男生,
名男生, 名女生,第二組有
名女生,第二組有 名男生,
名男生, 名女生.現在班主任老師要從第一組選出
名女生.現在班主任老師要從第一組選出 人,從第二組選出
人,從第二組選出 人,請他們在班會上和全班同學分享學習心得.
人,請他們在班會上和全班同學分享學習心得.
(Ⅰ)求選出的 人均是男生的概率;
人均是男生的概率;
(Ⅱ)求選出的 人中有男生也有女生的概率.
人中有男生也有女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
袋中有8個大小相同的小球,其中1個黑球,3個白球,4個紅球.
(I)若從袋中一次摸出2個小球,求恰為異色球的概率;
(II)若從袋中一次摸出3個小球,且3個球中,黑球與白球的個數都沒有超過紅球的個數,記此時紅球的個數為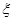 ,求
,求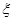 的分布列及數學期望E
的分布列及數學期望E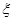 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對某校高一年級學生參加社區服務次數統計,隨機抽取了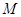 名學生作為樣本,得到這
名學生作為樣本,得到這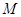 名學生參加社區服務的次數,根據此數據作出了頻數與頻率的統計表如下:
名學生參加社區服務的次數,根據此數據作出了頻數與頻率的統計表如下: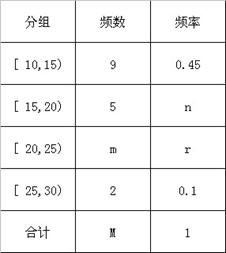
(1)求出表中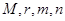 的值;
的值;
(2)在所取樣本中,從參加社區服務的次數不少于 次的學生中任選
次的學生中任選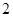 人,求至少一人參加社區服務次數在區間
人,求至少一人參加社區服務次數在區間 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個袋子里裝有7個球, 其中有紅球4個, 編號分別為1,2,3,4; 白球3個, 編號分別為2,3,4. 從袋子中任取4個球 (假設取到任何一個球的可能性相同).
(Ⅰ) 求取出的4個球中, 含有編號為3的球的概率;
(Ⅱ) 在取出的4個球中, 紅球編號的最大值設為X ,求隨機變量X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com