一名學生每天騎自行車上學，從家到學校的途中有5個交通崗，假設他在各交通崗遇到紅燈的事件是相互獨立的，并且概率都是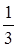
.
（1）求這名學生在途中遇到紅燈的次數ξ的分布列；
（2）求這名學生在首次遇到紅燈或到達目的地停車前經過的路口數η的分布列；
（3）這名學生在途中至少遇到一次紅燈的概率．
（1）
科目：高中數學
來源：
題型：解答題
袋子A、B中均裝有若干個大小相同的紅球和白球，從A中摸出一個紅球的概率是
科目：高中數學
來源：
題型：解答題
將一顆質地均勻的正方體骰子（六個面的點數分別為1，2，3，4，5，6）先后拋擲兩次，將得到的點數分別記為
科目：高中數學
來源：
題型：解答題
某學校為調查高二年級學生的身高情況，按隨機抽樣的方法抽取200名學生，得到男生身高情況的頻率分布直方圖（圖（1））和女生身高情況的頻率分布直方圖（圖（2））．已知圖（1）中身高在170~175cm的男生人數有48人．
科目：高中數學
來源：
題型：解答題
（1）從1,2,3,4,5五個數中依次取2個數，求這兩個數的差的絕對值等于1的概率；
科目：高中數學
來源：
題型：解答題
甲、乙兩隊在進行一場五局三勝制的排球比賽中，規定先贏三局的隊獲勝，并且比賽就此結束，現已知甲、乙兩隊每比賽一局，甲隊獲勝的概率為
科目：高中數學
來源：
題型：解答題
口袋中有大小、質地均相同的7個球，3個紅球，4個黑球，現在從中任取3個球。
科目：高中數學
來源：
題型：解答題
張師傅駕車從公司開往火車站，途徑4個公交站，這四個公交站將公司到火車站
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
的分布列為：
（2）
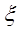
0 1 2 3 4 5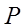 
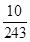
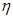的分布列為：
0 1 2 3 4 5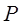 
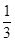
解析試題分析：（1）由于 ～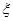
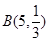，則
，
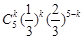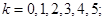
所以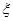的分布列為：
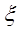
（2）0 1 2 3 4 5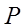 
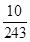
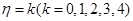也就是說{前
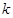個是綠燈，第
個是紅燈},
也就是說（5個均為綠燈)，則
，
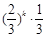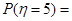
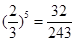；所以的分布列為：0 1 2 3 4 5 
練習冊系列答案
實驗報告系列答案
探究活動報告冊系列答案
家庭作業系列答案
課堂作業同步練習系列答案
教材完全解讀系列答案
課程達標測試卷系列答案
清華綠卡核心密卷創新測試卷系列答案
小學素質強化訓練AB卷系列答案
一路領航核心密卷系列答案
同步題組訓練與測評系列答案
相關習題
，從B中摸出一個紅球的概率為p.
（1） 從A中有放回地摸球，每次摸出一個，有3次摸到紅球即停止。
①求恰好摸5次停止的概率；
②記5次之內（含5次）摸到紅球的次數為
，求隨機變量的分布列及數學期望。
（2）若A、B兩個袋子中的球數之比為1：2，將A、B中的球裝在一起后，從中摸出一個紅球的概率是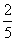
，求p的值。
.
（1）求直線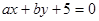
與圓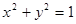
相切的概率；
（2）將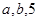
的值分別作為三條線段的長，求這三條線段能圍成等腰三角形的概率．
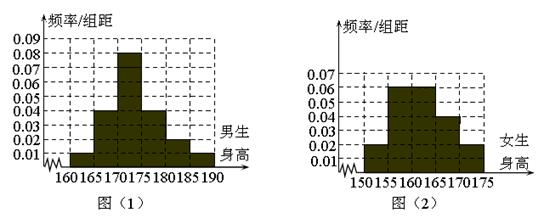（Ⅰ）在抽取的學生中，身高不超過165cm的男、女生各有多少人？并估計男生的平均身高。
（Ⅱ）在上述200名學生中，從身高在170~175cm之間的學生按男、女性別分層抽樣的方法，抽出7人，從這7人中選派4人當旗手，求4人中至少有一名女生的概率．
（2）△ABC中，∠B=60°，∠C=45°，高AD=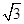
，在BC邊上任取一點M，求
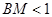的概率.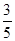
，乙隊獲勝的概率為
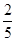，且每局比賽的勝負是相互獨立的，問：
（1）甲隊以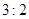
獲勝的概率是多少？
（2）乙隊獲勝的概率是多少？
(1)求取出的球顏色相同的概率；
(2)若取出的紅球數設為
，求隨機變量的分布列和數學期望。
分成5個路段，每個路段的駕車時間都是3分鐘，如果遇到紅燈要停留1分鐘，假設他在各
交通崗是否遇到紅燈是相互獨立的，并且概率都是
（1）求張師傅此行時間不少于16分鐘的概率
（2）記張師傅此行所需時間為Y分鐘，求Y的分布列和均值
同步練習冊答案
版權聲明：本站所有文章，圖片來源于網絡，著作權及版權歸原作者所有，轉載無意侵犯版權，如有侵權，請作者速來函告知，我們將盡快處理，聯系qq：3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號
