
已知函數f(x)= +ln x.
+ln x.
(1)當a= 時,求f(x)在[1,e]上的最大值和最小值;
時,求f(x)在[1,e]上的最大值和最小值;
(2)若函數g(x)=f(x)- x在[1,e]上為增函數,求正實數a的取值范圍.
x在[1,e]上為增函數,求正實數a的取值范圍.
(1) 最大值是0,最小值是ln 2-1 (2)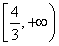
【解析】(1)當a=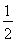 時,f(x)=
時,f(x)=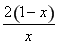 +ln x,
+ln x,
f′(x)=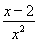 ,令f′(x)=0,得x=2.
,令f′(x)=0,得x=2.
∴當x∈[1,2)時,f′(x)<0,故f(x)在[1,2)上單調遞減;
當x∈(2,e]時,f′(x)>0,故f(x)在(2,e]上單調遞增.
∴f(x)在區間[1,e]上有唯一的極小值點,
故f(x)min=f(x)極小值=f(2)=ln 2-1.
又∵f(1)=0,f(e)=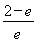 <0.
<0.
∴f(x)在區間[1,e]上的最大值f(x)max=f(1)=0.
綜上可知,函數f(x)在[1,e]上的最大值是0,最小值是ln 2-1.
(2)∵g(x)=f(x)-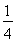 x=
x=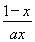 +ln x-
+ln x-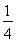 x,
x,
∴g′(x)=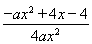 (a>0),
(a>0),
設φ(x)=-ax2+4ax-4,由題意知,只需φ(x)≥0在[1,e]上恒成立即可滿足題意.
∵a>0,函數φ(x)的圖象的對稱軸為x=2,
∴只需φ(1)=3a-4≥0,即a≥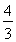 即可.
即可.
故正實數a的取值范圍為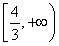 .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題3第2課時練習卷(解析版) 題型:填空題
已知數列{an}中,a1=1,an+1=(-1)n(an+1),記Sn為{an}前n項的和,則S2 013=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題2第2課時練習卷(解析版) 題型:解答題
設函數f(x)=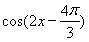 +2cos2x.
+2cos2x.
(1)求f(x)的最大值,并寫出使f(x)取最大值時x的集合;
(2)已知△ABC中,角A,B,C的對邊分別為a,b,c,若f(B+C)= ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題1第6課時練習卷(解析版) 題型:解答題
已知函數f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)當m= 時,求函數f(x)在區間[1,3]上的極小值;
時,求函數f(x)在區間[1,3]上的極小值;
(2)求證:函數f(x)存在單調遞減區間[a,b];
(3)是否存在實數m,使曲線C:y=f(x)在點P(1,1)處的切線l與曲線C有且只有一個公共點?若存在,求出實數m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題1第5課時練習卷(解析版) 題型:選擇題
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.現給出如下結論:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正確結論的序號是( )
A.①③ B.①④
C.②③ D.②④
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題1第4課時練習卷(解析版) 題型:解答題
首屆世界低碳經濟大會在南昌召開,本屆大會以“節能減排,綠色生態”為主題.某單位在國家科研部門的支持下,進行技術攻關,采用了新工藝,把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為400噸,最多為600噸,月處理成本y(元)與月處理量x(噸)之間的函數關系可近似地表示為y=x2-200x+80 000,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則國家至少需要補貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪專題復習與測試專題1第3課時練習卷(解析版) 題型:選擇題
若定義在R上的偶函數f(x)滿足f(x+2)=f(x),且x∈[0,1]時,f(x)=x,則方程f(x)=log3|x|的解有( )
A.2個 B.3個
C.4個 D.多于4個
查看答案和解析>>
科目:高中數學 來源:2014年高考數學理復習方案二輪作業手冊新課標·通用版專題四練習卷(解析版) 題型:填空題
在等比數列{an}中,a1+a2=20,a3+a4=40,則a5+a6等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com