
某企業員工500人參加“學雷鋒”志愿活動,按年齡分組:第1組[25,30),第2組[30,35),第3組[35,40),第4組[40,45),第5組[45,50],得到的頻率分布直方圖如下圖所示.
(Ⅰ)下表是年齡的頻數分布表,求正整數a,b的值;
| 區間 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人數 | 50 | 50 |  | 150 |  |
(I) ,
, .
.
(II)第1,2,3組分別抽取1人,1人,4人.
(III)至少有1人年齡在第3組的概率為 .
.
解析試題分析:(I)由題意可知 ,
, .
.
(II)根據各層在總體當中的占比與在樣本中的占比相等,求出年齡在第1,2,3組的人數. 因為第1,2,3組共有50+50+200=300人,
利用分層抽樣在300名學生中抽取 名學生,每組抽取的人數分別為:
名學生,每組抽取的人數分別為:
第1組的人數為 , 第2組的人數為
, 第2組的人數為 ,
,
第3組的人數為 , 所以第1,2,3組分別抽取1人,1人,4人. 6分
, 所以第1,2,3組分別抽取1人,1人,4人. 6分
(III) 設第1組的1位同學為 ,第2組的1位同學為
,第2組的1位同學為 ,第3組的4位同學為
,第3組的4位同學為 ,則從六位同學中抽兩位同學有15種可能.其中2人年齡都不在第3組的有1種可能.
,則從六位同學中抽兩位同學有15種可能.其中2人年齡都不在第3組的有1種可能.
所以至少有1人年齡在第3組的概率為 .設第1組的1位同學為
.設第1組的1位同學為 ,第2組的1位同學為
,第2組的1位同學為 ,第3組的4位同學為
,第3組的4位同學為 ,則從六位同學中抽兩位同學有:
,則從六位同學中抽兩位同學有:




 共
共 種可能. 10分
種可能. 10分
其中2人年齡都不在第3組的有: 共1種可能, 11分
共1種可能, 11分
所以至少有1人年齡在第3組的概率為 . 12
. 12
考點:本題主要考查頻率分布直方圖,頻率的概念及計算,古典概型概率的計算。
點評:典型題,統計中的抽樣方法,頻率直方圖,概率計算及分布列問題,是高考必考內容及題型。題中古典概型概率的計算思路明確,計數時,可采用“樹圖法”,避免重復和遺漏。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
一般來說,一個人腳掌越長,他的身高就越高。現對10名成年人的腳掌長 與身高
與身高 進行測量,得到數據(單位均為
進行測量,得到數據(單位均為 )作為樣本如下表所示.
)作為樣本如下表所示.
(1)在上表數據中,以“腳掌長”為橫坐標,“身高”為縱坐標,作出散點圖后,發現散點在一條直線附近,試求“身高”與“腳掌長”之間的線性回歸方程 ;
;
(2)若某人的腳掌長為 ,試估計此人的身高;
,試估計此人的身高;
(3)在樣本中,從身高180cm以上的4人中隨機抽取2人作進一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(參考數據: ,
, ,
, ,
, )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校為了解高二學生 、
、 兩個學科學習成績的合格情況是否有關, 隨機抽取了該年級一次期末考試
兩個學科學習成績的合格情況是否有關, 隨機抽取了該年級一次期末考試 、
、 兩個學科的合格人數與不合格人數,得到以下2
兩個學科的合格人數與不合格人數,得到以下2 2列聯表:
2列聯表:
| |  學科合格人數 學科合格人數 |  學科不合格人數 學科不合格人數 | 合計 |
 學科合格人數 學科合格人數 | 40 | 20 | 60 |
 學科不合格人數 學科不合格人數 | 20 | 30 | 50 |
| 合計 | 60 | 50 | 110 |
 學科合格”與“
學科合格”與“ 學科合格”有關;
學科合格”有關; 學科合格”的學生中任意抽取2人,記被抽取的2名學生中“
學科合格”的學生中任意抽取2人,記被抽取的2名學生中“ 學科合格”的人數為
學科合格”的人數為 ,求
,求 的數學期望.
的數學期望.
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(文科)某高校從參加今年自主招生考試的學生中隨機抽取容量為50的學生成績樣本,得頻率分布表如下:
| 組號 | 分組 | 頻數 | 頻率 |
| 第一組 | [230,235) | 8 | 0.16 |
| 第二組 | [235,240) | ① | 0.24 |
| 第三組 | [240,245) | 15 | ② |
| 第四組 | [245,250) | 10 | 0.20 |
| 第五組 | [250,255] | 5 | 0.10 |
| 合 計 | 50 | 1.00 | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
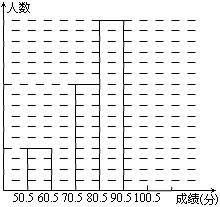
為了讓學生了解環保知識,增強環保意識,某中學舉行了一次“環保知識競賽”,共有900名學生參加了這次競賽. 為了解本次競賽成績情況,從中抽取了部分學生的成績(得分均為整數,滿分為100分)進行統計. 請你根據尚未完成并有局部污損的頻率分布表和頻數分布直方圖,解答下列問題:
(1)填充頻率分布表的空格(將答案直接填在表格內);
| 分組 | 頻數 | 頻率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合計 | 50 | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校從參加某次知識競賽的同學中,選取60名同學將其成績(百分制,均為整數)分成6組后,得到部分頻率分布直方圖(如圖),觀察圖中的信息,回答下列問題.
(Ⅰ)求分數在[70,80)內的頻率,并補全這個頻率分布直方圖;
(Ⅱ)根據頻率分布直方圖,估計本次考試的平均分;
(Ⅲ)若從60名學生中隨機抽取2人,抽到的學生成績在[40,70)記0分,記[70,100]記1分,用X表示抽取結束后的總記分,求X的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A、B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如下.記成績不低于90分者為“成績優秀”.
(1)在乙班樣本的20個個體中,從不低于86分的成績中隨機抽取2個,求抽出的2個至多一個“成績優秀”的概率;
(2)由以上統計數據填寫下面列聯表,并判斷是否有90%的把握認為:“成績優秀”與教學方式有關.
| | 甲班 (A方式) | 乙班 (B方式) | 總計 |
| 成績優秀 | | | |
| 成績不優秀 | | | |
| 總計 | | | |

 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2. 706 | 3. 841 | 5. 024 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)我校高二(1)班男同學有45名,女同學有15名,按照分層抽樣的方法組建了一個4人的課外興趣小組.
(1)求某同學被抽到的概率及課外興趣小組中男、女同學的人數;
(2)經過一個月的學習、討論,這個興趣小組決定選出兩名同學做某項實驗,方法是先從小組里選出1名同學做實驗,該同學做完后,再從小組內剩下的同學中選一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
(3)試驗結束后,第一次做試驗的同學得到的試驗數據為68,70,71,72,74,第二次做試驗的同學得到的試驗數據為69,70,70,72,74,請問哪位同學的實驗更穩定?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
為迎接建黨90周年,某班開展了一次“黨史知識競賽”,競賽分初賽和決賽兩個階段進行,在初賽后,把成績(滿分為100分,分數均為整數)進行統計,制成如圖頻率分布表: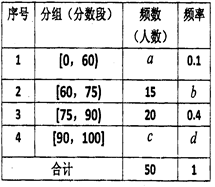
(1)求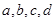 的值;
的值;
(2)決賽規則如下:為每位參加決賽的選手準備四道題目,選手對其依次作答,答對兩道就終止答題,并獲得一等獎,若題目答完仍然只答對一道,則獲得二等獎.某同學進入決賽,每道題答對的概率P的值恰好與頻率分布表中不少于90分的頻率的值相同.設該同學決賽中答題個數為X,求X的分布列以及X的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com