
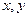 滿足
滿足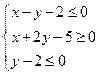 ,則
,則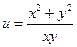 的取值范圍是 ( )
的取值范圍是 ( )A.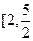 ] ] | B.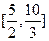 | C.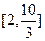 | D.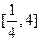 |
 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
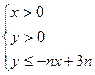 所表示的平面區(qū)域為
所表示的平面區(qū)域為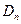 ,記
,記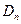 內(nèi)的格點(格點即橫坐
內(nèi)的格點(格點即橫坐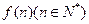 .
.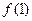 、
、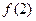 、
、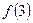 的值及
的值及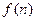 的表達式;
的表達式;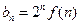 ,
,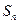 為
為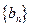 的前
的前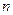 項和,求
項和,求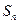 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 至少需要36單位的蛋白質(zhì)和42單位的鐵質(zhì),應使用甲、乙兩種藥片各幾片才能既
至少需要36單位的蛋白質(zhì)和42單位的鐵質(zhì),應使用甲、乙兩種藥片各幾片才能既 滿足營養(yǎng)要求又使費用最省?
滿足營養(yǎng)要求又使費用最省?查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
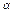 ,
,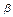 ,
,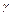 ∈R且
∈R且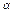 +
+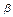 >0,
>0, 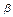 +
+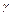 >0,
>0, 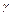 +
+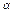 >0.試說明f(
>0.試說明f(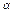 )+f(
)+f(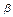 )+f(
)+f(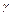 )的值與0的關系.
)的值與0的關系.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.7 | B.-1 |
| C.1 | D.-7 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com