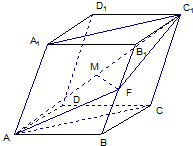
中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
已知四棱柱ABCD-A1B1C1D1中的底面是菱形，且∠DAB=∠A1AB=∠A1AD=60°，AD=1，AA1=a，F為棱BB的中點，M為線段AC的中點．設
AB
=
e1
，
AD
=
e2
，
AA1
=
e3
．試用向量法解下列問題：
（1）求證：直線MF∥平面ABCD；
（2）求證：直線MF⊥面A1ACC1；
（3）是否存在a，使平面AFC1與平面ABCD所成二面角的平面角是30°？如果存在，求出相應的a 值，如果不存在，請說明理由．（提示：可設出兩面的交線）
分析：（1）由：|
e1
|=|
e2
|=1，|
e3
|=a，
e 1
•
e2
=
1
2
，
e1
•
e3
=
e2
•
e3
=
1
2
a，
e1
e3
=
e2
e3
=
1
2
a，
AC1
=
e1
+
e2
+
e3
，
AM
=
1
2
（
e1
+
e2
+
e3
），
AF
=
AB
+
BF
=
AB
+
1
2
AA1
=
e1
+
1
2
e3
，
MF
=
AF
-
AM
=
1
2
（
e1
-
e2
），
DB
=
AB
-
AD
=
e1
-
e2
=2
MF
，由此能證明直線MF∥平面ABCD．
（2）由
MF
•
AA1
=（
e1
-
e2
）•
1
2
e3
=0，
MF
•
AC
=（
e1
-
e2
）（
e1
+
e2
+
e3
）•
1
2
=0，知MF⊥AA1，MF⊥AC，AC和AA1是面ABCD內的相交直線，由此能證明直線MF⊥面A1ACC1．
（3）設平面AFC1與平面ABCD的交線為c，兩平面有一個公共點A，故A在直線c上；MF在面AFC1內，直線MF∥平面ABCD，有MF∥直線c，由直線MF⊥面A1ACC1，直線AC和直線AC1在平面A1ACC1內，知平面AFC1與平面ABCD所成二面角的平面角是∠C1AC由此能推導出不存在這樣的a值，使平面AFC1與平面ABCD所成二面角的平面角是30°．
解答：（1）證明：|
e1
|=|
e2
|=1，
|
e3
|=a，
e 1
•
e2
=
1
2
，
e1
•
e3
=
e2
•
e3
=
1
2
a，（2分）
AC1
=
e1
+
e2
+
e3
，
AM
=
1
2
（
e1
+
e2
+
e3
），
AF
=
AB
+
BF
=
AB
+
1
2
AA1
=
e1
+
1
2
e3
，
MF
=
AF
-
AM
=
1
2
（
e1
-
e2
），（3分）
DB
=
AB
-
AD
=
e1
-
e2
=2
MF
，
DB在面ABCD內，MF在面ABCD外，
∴直線MF∥平面ABCD；（4分）
（2）證明：
MF
•
AA1
=（
e1
-
e2
）•
1
2
e3
=0，（5分）
MF
•
AC
=（
e1
-
e2
）•（
e1
+
e2
+
e3
）•
1
2
=0，（6分）
∴MF⊥AA1，MF⊥AC，AC和AA1是面ABCD內的相交直線，
∴直線MF⊥面A1ACC1；（7分）
（3）解：設平面AFC1與平面ABCD的交線為c，兩平面有一個公共點A，
∴A在直線c上；MF在面AFC1內，直線MF∥平面ABCD，有MF∥直線c，
由2）知，直線MF⊥面A1ACC1，直線AC和直線AC1在平面A1ACC1內，
∴MF⊥AC1，MF⊥AC，因此，有AC1⊥直線c，AC⊥直線c，
平面AFC1與平面ABCD所成二面角的平面角是∠C1AC，（10分）
假設存在這樣的a，使∠C1AC=30°，
則cos30°=cos＜
AC 1
，
AC
＞
=
    <menu id="wneng"></menu>
      AC1
      •
      
				練習冊系列答案
		
      


      
			
			
			
		
	

		

		





			
		
		
				
		
				
		
      
              
                
      
                  年級
                  高中課程
                  年級
                  初中課程
                
      
                
      
                  高一
                  高一免費課程推薦！
                  初一
                  初一免費課程推薦！
                
      
               
                
      
                  高二
                  高二免費課程推薦！
                  初二
                  初二免費課程推薦！
                
      
               
                
      
                  高三
                  高三免費課程推薦！ 
                  初三
                  初三免費課程推薦！
                
      
               
                
      
                  
                
      
                    
            
      
			

					
      
				相關習題
			
      
						
		
      
			
      
				科目：高中數學
				來源：
				題型：
			
      

						
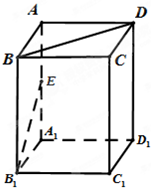      已知四棱柱ABCD-A1B1C1D1中，側棱AA1⊥底面ABCD，AA1=2，底面四邊形ABCD的邊長均大于2，且∠DAB=45°，點P在底面ABCD內運動且在AB，AD上的射影分別為M，N，若|PA|=2，則三棱錐P-D1MN體積的最大值為（　　）
      

			
      

			
      
			查看答案和解析>>		
      
				
		
      
			
      
				科目：高中數學
				來源：
				題型：
			
      

						
      已知四棱柱ABCD-A1B1C1D1的底面是邊長為1的正方形，側棱垂直底邊ABCD四棱柱，AA1=2，E是側棱AA1的中點，求
      （1）求異面直線BD與B1E所成角的大小；
      （2）求四面體AB1D1C的體積．
      

			
      

			
      
			查看答案和解析>>		
      
				
		
      
			
      
				科目：高中數學
				來源：
				題型：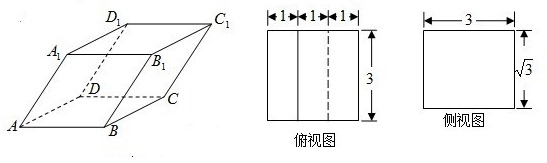
			
      

						
      （2012•江門一模）如圖，已知四棱柱ABCD-A1B1C1D1的俯視圖是邊長為3的正方形，側視圖是長為3寬為
      		3
      的矩形．
      （1）求該四棱柱的體積；
      （2）取DD1的中點E，證明：面BCE⊥面ADD1A1．
      

			
      

			
      
			查看答案和解析>>		
      
				
		
      
			
      
				科目：高中數學
				來源：
				題型：
			
      

						
      精英家教網如圖，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AA1=3，∠BAA1=60°，E為棱C1D1的中點，則
      AB
      •
      AE
      =
       
      ．
      

			
      

			
      
			查看答案和解析>>		
      
			
	



      
	







      <object id="wneng"><button id="wneng"></button></object>
      <dfn id="wneng"></dfn>
        <menuitem id="wneng"></menuitem>
        <menuitem id="wneng"></menuitem>