Question

設函數的定義域為R, 當x＜0時, ＞1, 且對于任意的實數, 有

成立. 又數列滿足, 且

(1)求證: 是R上的減函數；

(2)求的值；

  (3)若不等式≥k ?對一切均成立, 求的最大值.

Answer 1

解析: (1)由題設, 令x= -1, y=0, 可得f(-1)=f(-1)f(0), ∴ f(0)=1. 故a₁=f(0)=1

     當x＞0時, -x＜0, ∴ f(-x)＞1, 且 1=f(0)=f(x)f(-x), 故得 0＜f(x)＜1

     從而可得f(x)＞0, x∈R

     設x₁, x₂∈R, 且x₁＜x₂, 則x₂-x₁＞0, 故f(x₂-x₁)＜1, f(x₁)＞0

     從而f(x₁) -f(x₂)=f(x₁) -f(x₁+x₂-x₁)=f(x₁) -f(x₁)f(x₂-x₁)=f(x₁)[1-f(x₂-x₁)]＞0

     即f(x₁)＞f(x₂), ∴函數f(x)在R上是減函數.

   (2)由f(a_n+1)=, 得f(a_n+1)f( -2-a_n)=1, 即f(a_n+1-a_n-2)=f(0)

     由f(x)的單調性, 故a_n+1-a_n-2=0 即a_n+1-a_n=2  (n∈N^*)

     因此, {a_n}是首項是1, 公差為2的等差數列, 從而a_n=2n-1, ∴ a₂₀₀₇=4013

   (3)設g(n)=, 則g(n)＞0, 且k≤g(n)對n∈N^*恒成立.

     由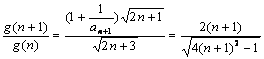＞1, 即g(n+1)＞g(n),

∴ g(n)在N^*上為單調遞增函數,  故g(n)≥g(1)=

     因此, k≤, 即k的最大值為