（1）已知
，求證：
；
（2）已知
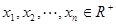，且
，
求證：
．
證明見解析.
解析試題分析：（1）本題證明只要利用作差法即可證得；（2）這個不等式比較復雜，考慮到不等式的形式，我們可用數學歸納法證明，關鍵在
時的命題如何應用
時的結論，
中要把兩個括號合并成一個，又能應用時的結論證明時的結論，當
時，結論已經成立，當
時，在
中可找到一個，不妨設為
，使
，即
，從而有
，這樣代入進去可證得時結論成立.
（1）因為
，所以
，即
； 2分
（2）證法一（數學歸納法）：（ⅰ）當
時，
，不等式成立． 4分
（ⅱ）假設時不等式成立，即
成立. 5分
則時，若
，則命題成立；若
，則
中必存在一個數小于1，不妨設這個數為
，從而，即．
同理可得，
所以
故時，不等式也成立． 9分
由（ⅰ）（ⅱ）及數學歸納法原理知原不等式成立. 10分
證法二：（恒等展開）左右展開，得
由平均值不等式，得
8分
故
． 10分
考點：（1）比較法證不等式；（2）數學歸納法證不等式.
陽光同學一線名師全優好卷系列答案科目：高中數學 來源： 題型：解答題
給出四個等式：
1＝1
1－4＝－(1＋2)
1－4＋9＝1＋2＋3
1－4＋9－16＝－(1＋2＋3＋4)
……
（1）寫出第5,6個等式，并猜測第n(n∈N*)個等式
（2）用數學歸納法證明你猜測的等式．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知數列{bn}是等差數列，b1＝1，b1＋b2＋…＋b10＝145.
(1)求數列{bn}的通項公式bn；
(2)設數列{an}的通項an＝loga
(其中a＞0且a≠1)．記Sn是數列{an}的前n項和，試比較Sn與
logabn＋1的大小，并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某少數民族的刺繡有著悠久的歷史，如圖(1)、(2)、(3)、(4)為她們刺繡最簡單的四個圖案，這些圖案都是由小正方形構成，小正方形數越多刺繡越漂亮．現按同樣的規律刺繡(小正方形的擺放規律相同)，設第n個圖形包含f(n)個小正方形．
(1)求出f(5)的值；
(2)利用合情推理的“歸納推理思想”，歸納出f(n＋1)與f(n)之間的關系式，并根據你得到的關系式求出f(n)的表達式；
(3)求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：填空題
在解決問題：“證明數集
沒有最小數”時，可用反證法證明．
假設
是
中的最小數，則取
，可得：
，與假設中“
是中的最小數”矛盾！那么對于問題：“證明數集
沒有最大數”，也可以用反證法證明．我們可以假設
是
中的最大數，則可以找到
▲ （用
，
表示），由此可知
，
，這與假設矛盾！所以數集沒有最大數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
≤
.
，
，
．
時，試比較
與
的大小關系；
與
的大小關系，并給出證明．
中，已知
，
，
(
，
)．
，
時，分別求
的值，判斷
是否為定值，并給出證明；
，使得
為完全平方數．
計算
由此推測出
的計算公式，并用數學歸納法證明.